نسبتهای مثلثاتی دوبرابر یک زاویه
میخواهیم مقدار تابع مثلثاتی را برحسب نسبتهای مثلثاتی زاویهی بدست آوریم.
ایدهی کلی
یک ایدهٔ موثر در بسیاری از مسئلهها (نه فقط مثلثات) این است:
یک کمیت را در یک محیط مناسب تعریف کن
و بعد آن را به دو روش متفاوت حساب کن.
بازنویسی (Recasting): ترجمهٔ مسئله به زبان هندسه
پس نیاز داریم یک محیط داشته باشیم که:
1) زاویهٔ و دوبرابرش را در همان فضا بتوانیم ببینیم،
2) کسینوسها هم در آن محیط معنی هندسی واضحی داشته باشند.
این دقیقاً همان جایی است که دایره بهترین انتخاب است.
انتخاب صحنهٔ مناسب: دایره
حالا سؤال طبیعی این است: چرا دایره اینقدر انتخاب مناسبی برای این مسئله است؟ پاسخ در یک قضیهٔ بسیار ساده نهفته است. قضیهای که احتمالا قبلتر آن را دیدهاید:
اندازهٔ زاویهٔ محاطی نصفِ اندازهٔ زاویهٔ مرکزیِ متناظر با همان کمان است.
این دقیقاً همان چیزی است که ما نیاز داریم.
- یک زاویهٔ مرکزی با اندازهٔ رسم کنیم،
- و روی همان کمان، یک زاویهٔ محاطی با اندازهٔ بسازیم.
به این ترتیب، و بهطور همزمان و کاملاً طبیعی در یک صحنه حضور دارند.
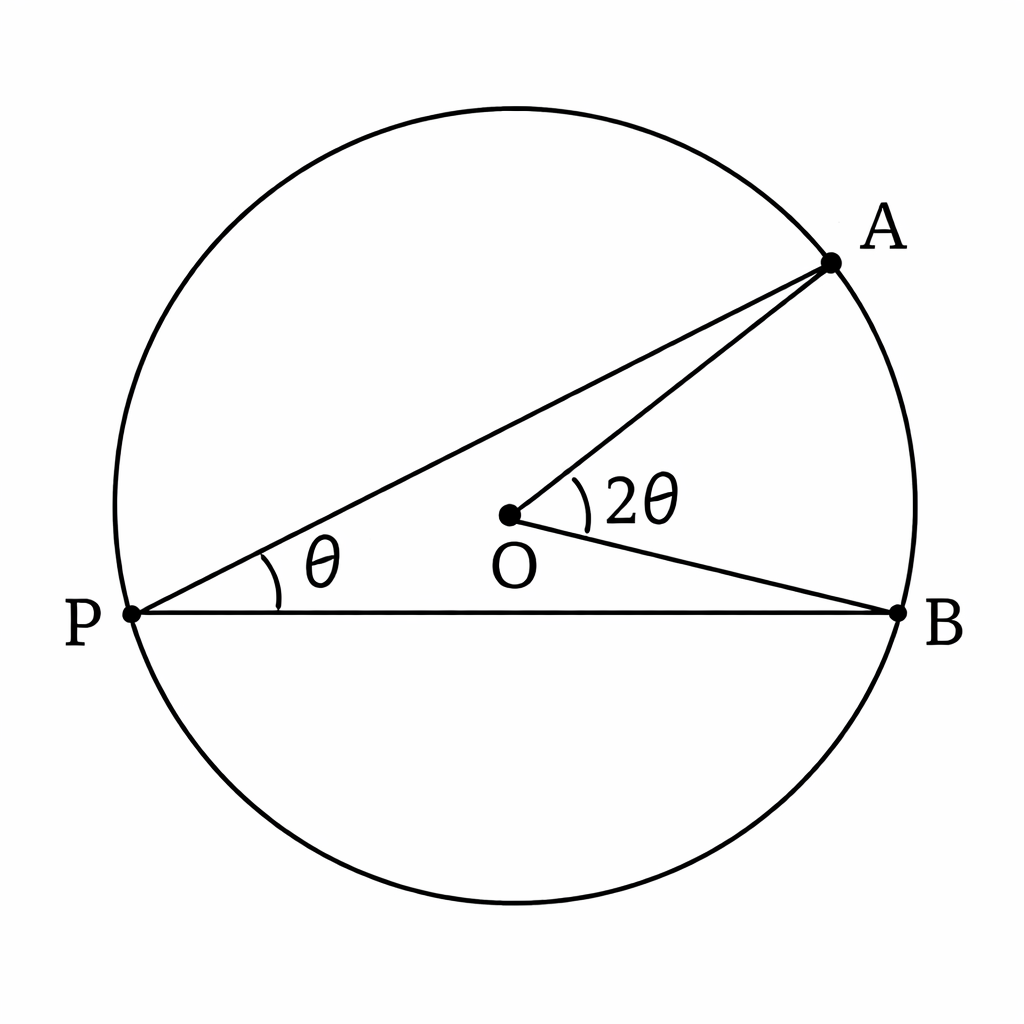
یک سادهسازی هوشمندانه در شکل
بیایید فرض کنیم خط قطر دایره باشد؛ یعنی نقطهٔ (مرکز دایره) دقیقاً روی پارهخط قرار بگیرد.
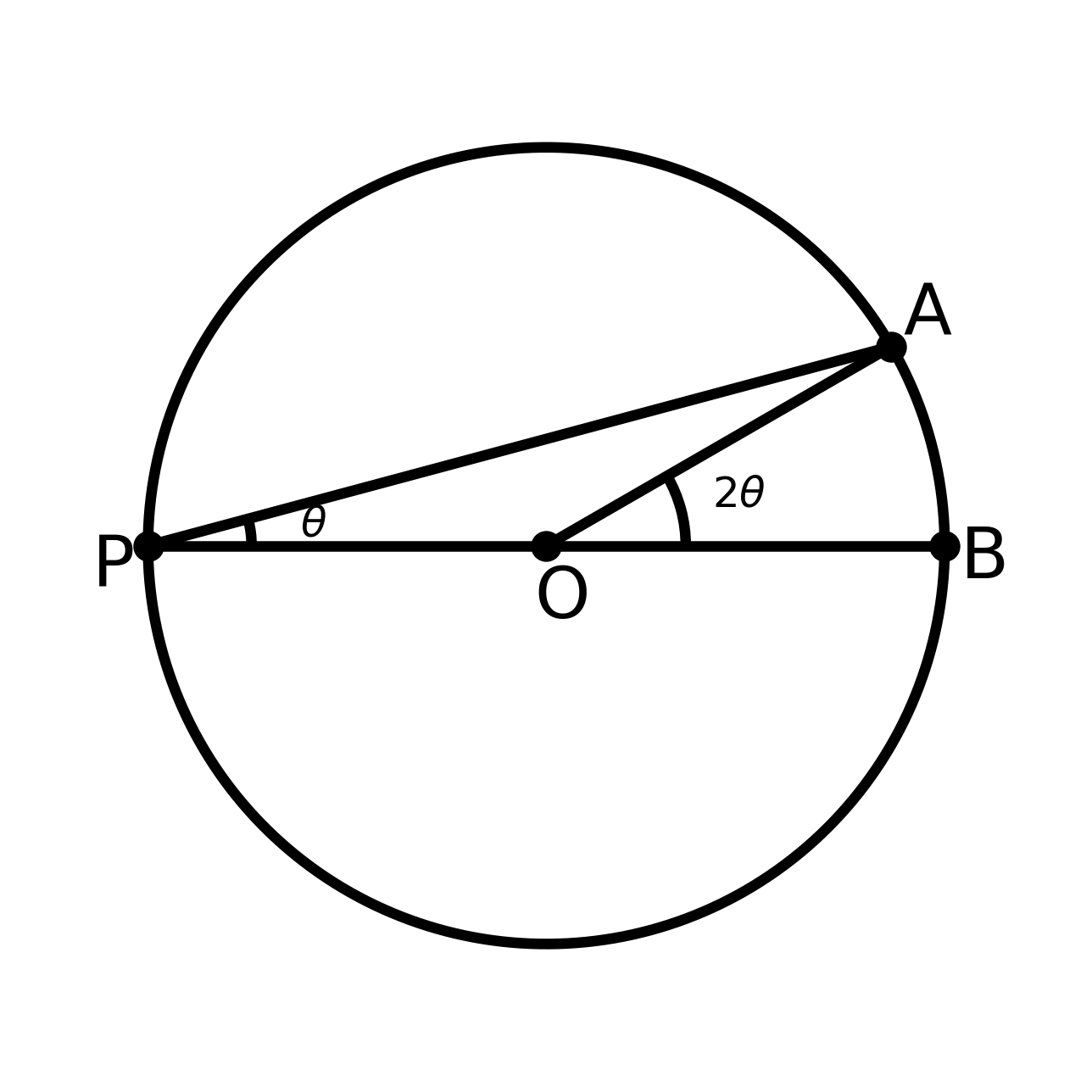
همچنین فرض میکنیم شعاع دایره برابر باشد. این انتخاب محاسبات را سادهتر میکند و هیچچیز از کلیت مسئله کم نمیکند.
حالا کمی به شکل نگاه کنید. در این مرحله، هدف ما این است که نسبتهای مثلثاتی را به طولها ربط بدهیم.
اولین خطِ کمکی طبیعی که به ذهن میرسد این است که از نقطهٔ یک خط عمود بر قطر رسم کنیم و پای عمود را روی مشخص کنیم. (آن را بنامید).
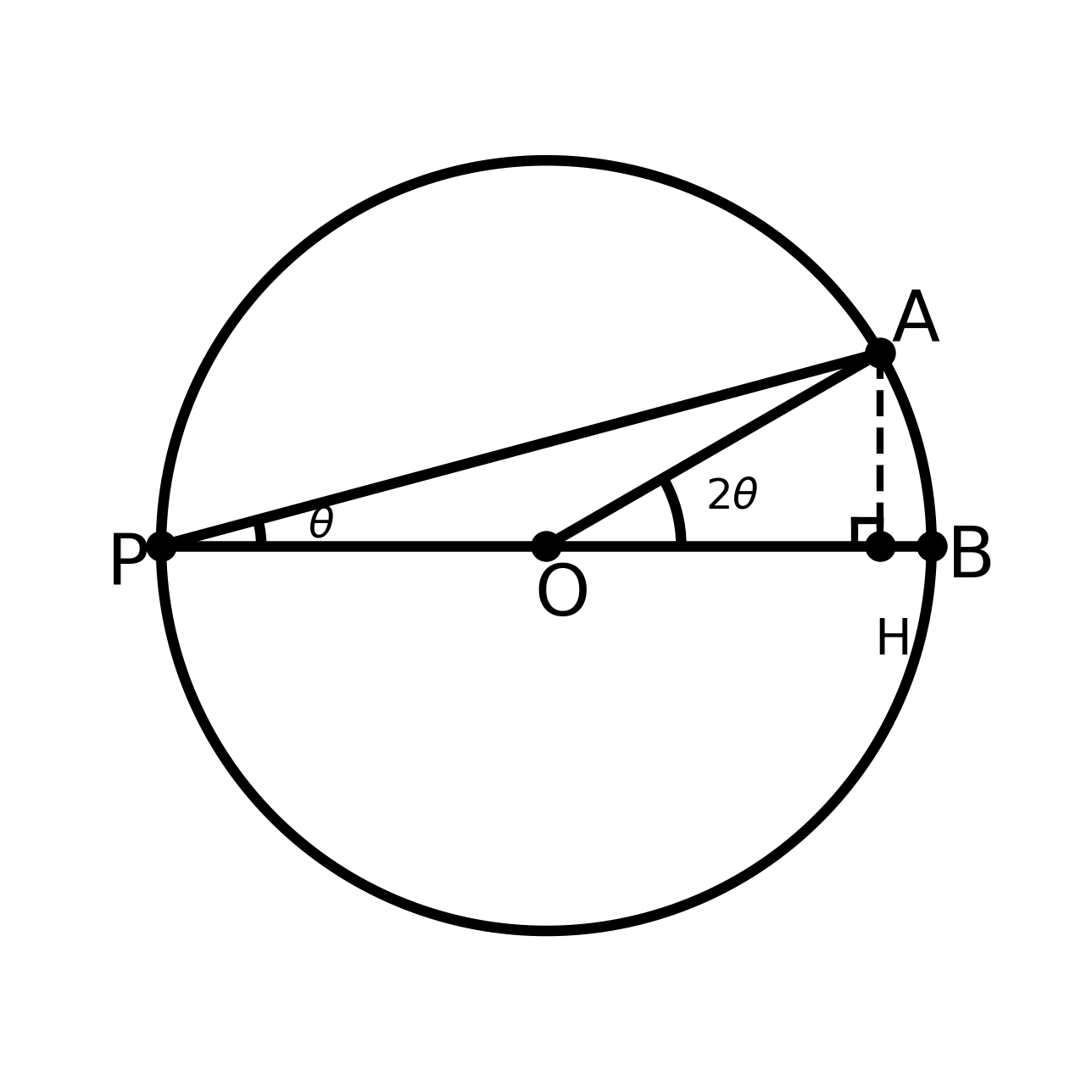
محاسبهی طول پارهخطها
حالا که شکل را آماده کردهایم، وقت آن است که طولها را وارد بازی کنیم.
فرض کنید از نقطهٔ عمودی بر قطر رسم کردهایم و پای عمود را نامیدهایم. پس و نقطهٔ روی قطر قرار دارد.
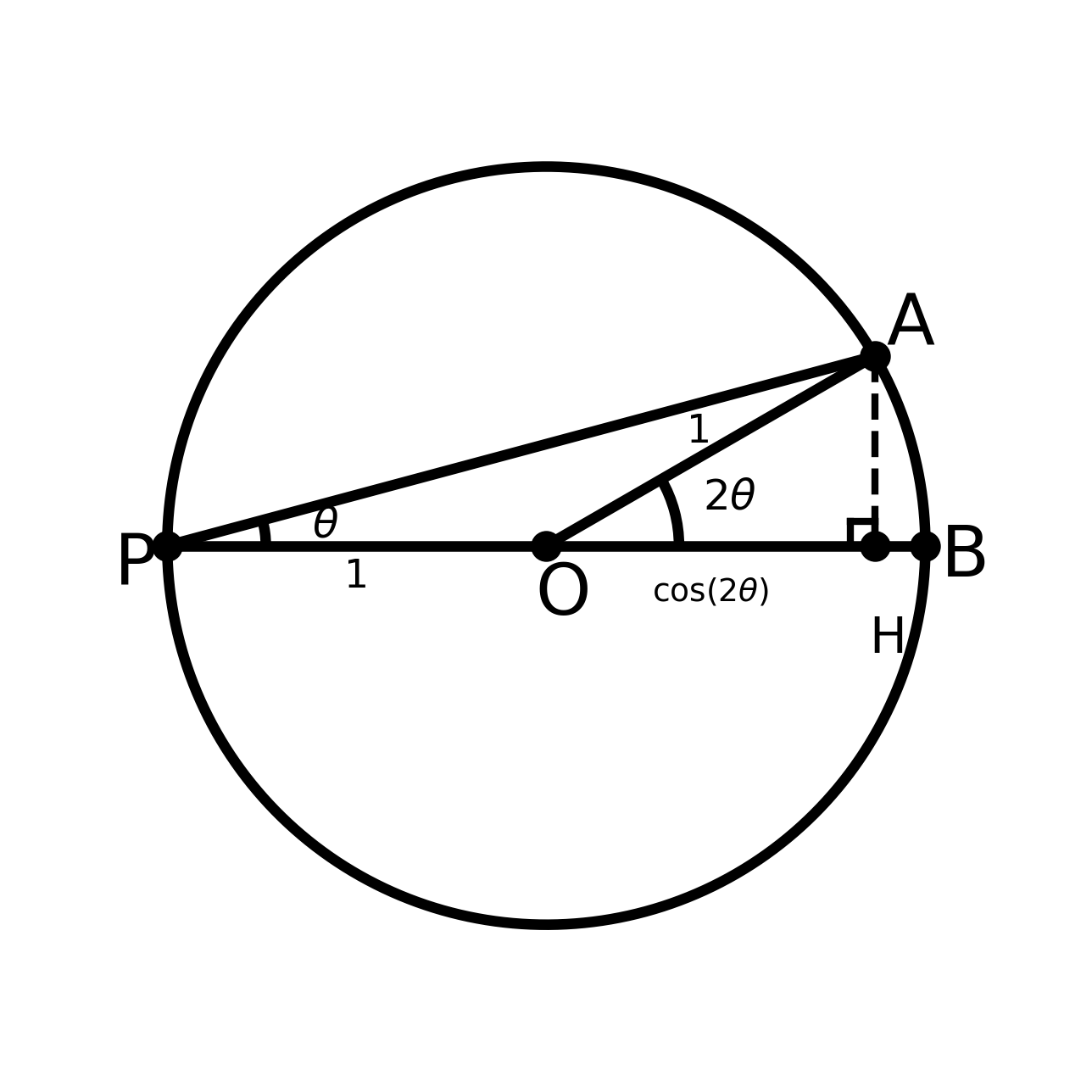
ابتدا به مثلثی نگاه میکنیم که زاویهٔ مرکزی را در خود دارد. در مثلث :
- وتر شعاع دایره است و طولش برابر است،
- زاویهٔ برابر است.
ضلع مجاور زاویهٔ در مثلث قائمالزاویهای با وتر است. بنابراین:
حالا به مثلث دیگری نگاه میکنیم؛ مثلثی که دقیقاً زاویهٔ را در خود دارد. این مثلث چیزی نیست جز مثلث .
در این مثلث:
- زاویهٔ رأس برابر است،
- عمود بر است،
- و وتر مثلث محسوب میشود.
پس طبق تعریف کسینوس داریم:
نقطهٔ روی قطر قرار دارد، و نقطهٔ مرکز دایره است. پس پارهخط را میتوان بهصورت مجموع دو پارهخط نوشت:
از آنجا که شعاع دایره را برابر فرض کردهایم، داریم: و از محاسبهٔ قبلی:
پس نتیجه میگیریم:
برای محاسبهٔ طول ، یک خط کمکی دیگر به شکل اضافه میکنیم.
از نقطهٔ (مرکز دایره) یک عمود بر پارهخط رسم میکنیم و پای عمود را مینامیم. پس:
به دو مثلث و نگاه کنید.
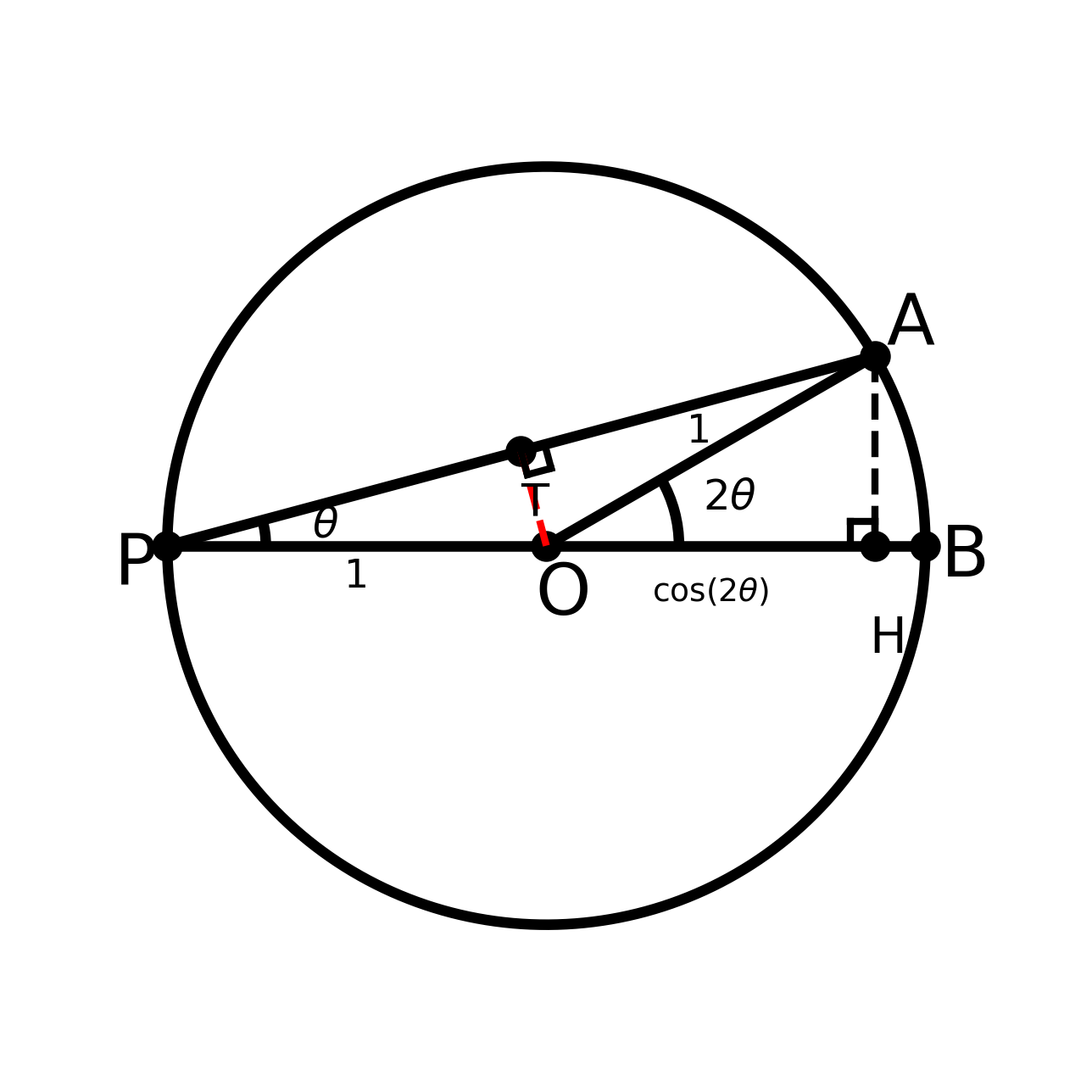
در این دو مثلث داریم:
- (هر دو شعاع دایرهاند)،
- ضلع مشترک است،
- و هر دو مثلث قائمالزاویهاند.
پس این دو مثلث همنهشت هستند. در نتیجه، نقطهٔ وسط پارهخط است؛ یعنی:
حالا به مثلث قائمالزاویهٔ نگاه میکنیم.
در این مثلث:
- زاویهٔ رأس برابر است،
- وتر مثلث است که طولش است،
- و ضلع مجاور زاویهٔ است.
پس طبق تعریف کسینوس داریم:
بنابراین:
از آنجا که وسط است، داریم:
گام پایانی: رسیدن به «فرمول طلایی»
حالا همهٔ قطعات پازل آمادهاند. رابطهای که در مثلث بهدست آوردیم این بود:
از گامهای قبل داریم:
این دو را در رابطهٔ بالا جایگذاری میکنیم:
دو طرف را در ضرب میکنیم:
و در نهایت به رابطهٔ مشهور میرسیم:
جمعبندی: استراتژی حل مسئله چه بود؟
در این حل، هدف اصلی حفظ یا بازتولید یک فرمول نبود؛ بلکه تمرین یک روش فکر کردن بود.
کارهایی که انجام دادیم، اینها بودند:
- مسئله را از زبان جبری به زبان هندسی بازنویسی کردیم (recasting)،
- صحنهای انتخاب کردیم که ساختار مسئله بهطور طبیعی در آن ظاهر شود (دایره)،
- از یک قضیهٔ ساده اما قدرتمند استفاده کردیم (زاویهٔ محاطی و مرکزی)،
- دو خط هوشمندانه و سادهی کمکی اضافه کردیم.
- یک کمیت مشترک را به دو روش متفاوت محاسبه کردیم،
- و با مقایسهی این دو محاسبه، نتیجه را استخراج کردیم.
این دقیقاً همان الگویی است که در بسیاری از حلهای خوب دیده میشود.