مسئلهٔ مجموع دو تاس
یک تاس استاندارد روی شش وجهش عددهای ۱ تا ۶ را دارد (روی هر وجه یک عدد صحیح). وقتی دو تاس استاندارد را میاندازیم، محاسبهٔ احتمال مجموعها ساده است:
- احتمال اینکه مجموع برابر ۲ شود، $\tfrac{1}{36}$ است،
- احتمال اینکه مجموع برابر ۷ شود، $\tfrac{1}{6}$ است،
- و به همین شکل برای سایر مجموعها نیز توزیع احتمال مشخص است.
پرسش اصلی این است:
آیا میتوان دو تاس ششوجهیِ «غیراستاندارد» ساخت (لزومی ندارد شبیه هم باشند) که روی وجههایشان عددهای صحیحِ مثبتِ دلخواه نوشته شده باشد، اما وقتی این دو تاس را میاندازیم و فقط مجموع دو عدد برای ما اهمیت دارد، رفتار آنها از نظر «توزیع احتمال مجموعها» کاملاً شبیه یک جفت تاس استاندارد باشد؟
به بیان دیگر:
- ممکن است روی یکی از تاسها عدد ۸ نوشته شده باشد،
- یا روی یکی از تاسها عدد ۳ دو بار تکرار شده باشد،
- یا اصلاً ترتیب و پراکندگی عددها روی دو تاس عجیب و نامعمول باشد،
اما احتمال مجموع ۲ همچنان برابر $\tfrac{1}{36}$ باشد و احتمال مجموع ۷ همچنان برابر $\tfrac{1}{6}$ و به همین ترتیب، تمام احتمالهای دیگر نیز دقیقاً همان باشند که برای دو تاس معمولی بهدست میآیند. آیا ساخت چنین تاسهایی ممکن است؟
بازنگری در مسئله (Recasting): دیدن دوبارهٔ آنچه پیش چشممان است
گاهی مسئله سخت است، نه چون ذاتاً پیچیده است، بلکه چون از زاویهٔ نادرست به آن نگاه میکنیم.
یک تغییر کوچک در زاویهٔ دید—گاهی حتی یک نگاه جانبی—کافی است تا مسئلهای مبهم و دشوار، به مسئلهای ساده و طبیعی تبدیل شود.
این تغییر زاویه همان چیزی است که در حل مسئله به آن میگوییم: Recasting — بازچینی یا بازنگری مسئله. یعنی مسئله را از نو بسازیم؟ نه. یعنی چگونه نگاه کردن به مسئله را عوض کنیم.
تغییر زاویهٔ دید
مسئلهای که از یک زاویه گیجکننده است، ممکن است از زاویهای دیگر کاملاً شفاف باشد. گاهی فقط کافی است چند دقیقه وقت بگذاریم و بپرسیم:
«زاویهٔ طبیعی این مسئله چیست؟
این سؤال را چطور باید ببینم؟»
همین چند دقیقه معمولاً سود بزرگی دارد.
تصویر بکش!
یکی از سادهترین ابزارهای بازنگری، تصویرکشیدن است. ترجمهٔ یک مسئلهٔ کلامی به یک شکل یا جدول، در بسیاری از موارد ساختارش را روشن میکند. گاهی تنها با کشیدن یک نمودار یا جدول، نیمهٔ پنهان مسئله آشکار میشود. اگر تصویر کمک نکرد، باز هم راه بسته نیست.
اگر تصویر کافی نبود، مسئله را جور دیگری بازنویسی کن
بازنگری فقط تصویرکشیدن نیست. گاهی باید مسئله را به «زبانی دیگر» بیان کرد:
- پرسش ترکیباتی را به یک گزارهٔ نظریهٔ اعداد تبدیل کنیم،
- یا مسئلهای هندسی را به شکل جبری بنویسیم.
بسیاری از پیشرفتهای بزرگ ریاضی دقیقاً از همین تغییر زبان آمدهاند. آنجا که کسی فهمیده مسئلهٔ هندسی را میتوان عددی کرد، یا مسئلهٔ عددی را میتوان هندسی خواند، دروازهٔ تازهای گشوده شده است.
بازنگری یعنی همین:
اینکه مسئله را در قالبی قرار دهیم که نفس مسئله خودش را بهتر نشان دهد.
توزیع مجموع دو تاس استاندارد
دو تاس معمولی داریم که روی هر کدام از آنها عددهای ۱ تا ۶ نوشته شده است. هر دو تاس را میاندازیم و مجموع دو عدد ظاهرشده را در نظر میگیریم.
- کوچکترین مجموع ممکن ۲ است (هر دو تاس ۱ بیایند).
- بزرگترین مجموع ممکن ۱۲ است (هر دو تاس ۶ بیایند).
هر تاس ۶ حالت دارد، پس دو تاس با هم:
\[6 \times 6 = 36\]حالت ممکن ایجاد میکنند. برای روشنتر شدن موضوع، کافی است جدول ۶×۶ حالتها را رسم کنیم؛ در هر خانه مجموع دو عدد نوشته شده است:
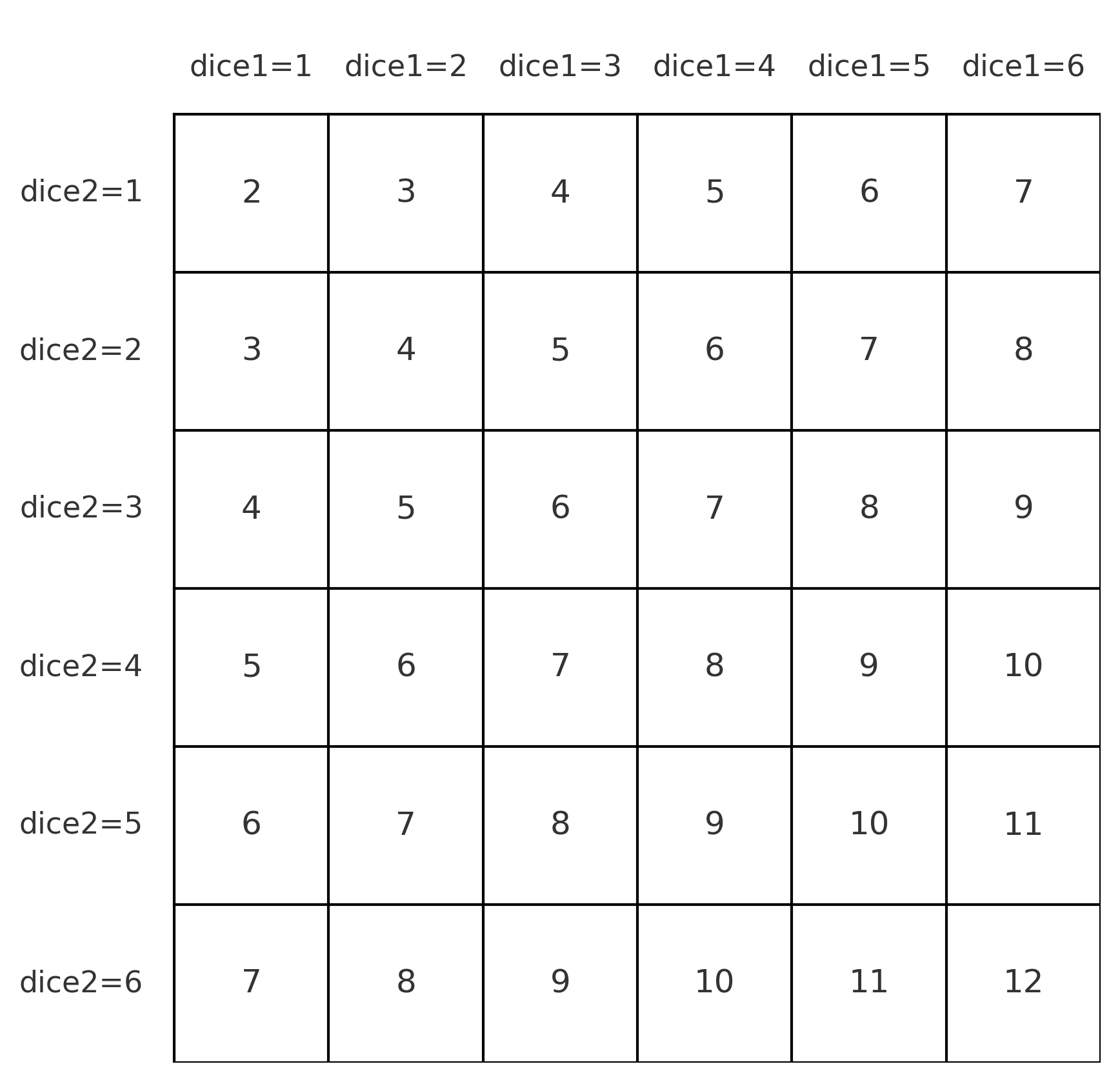
در این جدول:
-
فقط یک خانه مجموع ۲ میدهد (۱+۱)، پس احتمال آن $\frac{1}{36}$ است.
-
مجموع ۳ در دو خانه دیده میشود (۱+۲ و ۲+۱)، پس احتمال آن $\frac{2}{36}$ است.
-
مجموع ۴ در سه خانه ظاهر میشود، مجموع ۵ در چهار خانه و همین روند ادامه دارد تا مجموع ۷ که در ۶ حالت ممکن است.
-
سپس دوباره تعداد حالات کم میشود تا میرسیم به مجموع ۱۲ که درست مانند مجموع ۲ فقط در یک خانه (۶+۶) ظاهر شده است.
اکنون الگو کاملاً روشن است:
\[1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1\]پس توزیع مجموع دوتاس معمولی بهاین صورت میشود:
\[\begin{array}{c|ccccccccccc} \text{sum} & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline p(\text{sum}) & \tfrac{1}{36} & \tfrac{2}{36} & \tfrac{3}{36} & \tfrac{4}{36} & \tfrac{5}{36} & \tfrac{6}{36} & \tfrac{5}{36} & \tfrac{4}{36} & \tfrac{3}{36} & \tfrac{2}{36} & \tfrac{1}{36} \end{array}\]بازنویسی تاسها بهصورت چندجملهای
تا اینجا توزیع مجموع دو تاس استاندارد را دقیقاً میدانیم. سؤال ما این بود:
آیا میتوان دو تاسِ غیراستاندارد ساخت که از نظر مجموعها
دقیقاً مثل دو تاس استاندارد رفتار کنند؟
برای نزدیکشدن به پاسخ، مسئله را از دنیای «وجوه تاس» به دنیای «چندجملهایها» منتقل میکنیم.
گام اول: نگاهکردن به یک تاس، نه دو تاس
فعلاً فقط به یک تاس استاندارد نگاه کنیم. روی این تاس عددهای ۱ تا ۶ نوشته شده است. اگر بخواهیم «توزیع خروجی» این تاس را بهشکلی فشرده بنویسیم، میتوانیم بگوییم:
- احتمال آمدن ۱ برابر است با $\tfrac{1}{6}$،
- احتمال آمدن ۲ برابر است با $\tfrac{1}{6}$،
- …
- احتمال آمدن ۶ نیز $\tfrac{1}{6}$ است.
حالا بهجای نوشتن اینها در قالب جدول احتمال، یک کار جالب میکنیم: همهچیز را در قالب یک چندجملهای مینویسیم.
برای تاس استاندارد، چندجملهای زیر را در نظر بگیرید:
\[P(x) = x^1 + x^2 + x^3 + x^4 + x^5 + x^6.\]در این نمایش:
- هر جملهٔ $x^k$ یعنی «روی تاس، عدد $k$ روی یکی از وجهها نوشته شده است»،
- ضریب هر جمله (که اینجا همهجا ۱ است) یعنی «چند بار این عدد روی تاس ظاهر شده».
اگر تاسی داشتیم که مثلاً روی آن عددهای
\[1, 2, 2, 3, 5, 8\]نوشته شده بود، چندجملهای متناظر با آن میشد:
\[Q(x) = x^1 + 2x^2 + x^3 + x^5 + x^8.\](چون «۲» دو بار آمده است.)
گام دوم: مجموع اعداد دو تاس = ضرب دو چندجملهای
حالا دو تاس را همزمان میاندازیم. فرض کنیم تاس اول با چندجملهای $P(x)$ و تاس دوم با چندجملهای $Q(x)$ نمایش داده شود. وقتی دو تاس را میاندازیم، اگر تاس اول $a$ بیاورد و تاس دوم $b$، مجموع میشود $a + b$.
در زبان چندجملهایها، این یعنی داریم جملهٔ $x^a$ (از تاس اول) و جملهٔ $x^b$ (از تاس دوم) را با هم ترکیب میکنیم.
حاصل این ترکیب، جملهٔ
است. بنابراین:
توزیع مجموع دو تاس، همان ضریبهای حاصلضربِ چندجملهایهای دو تاس است.
بهعبارت دقیقتر، اگر تاس اول با $P(x)$ و تاس دوم با $Q(x)$ نشان داده شود، چندجملهای
\[R(x) = P(x)\,Q(x)\]چنین خاصیتی دارد که:
- ضریبِ $x^k$ در $R(x)$
برابر است با «تعداد حالتهایی که مجموع دو تاس برابر $k$ میشود».
این همان همگشت (convolution) توزیعهای دو تاس است، اما در زبان جبر: ضرب چندجملهایها.
گام سوم: چندجملهای مخصوص دو تاس استاندارد
برای دو تاس استاندارد، هر دو یکساناند و چندجملهای هر کدام:
\[P(x) = x + x^2 + x^3 + x^4 + x^5 + x^6.\]پس چندجملهای مجموعِ آنها:
\[R(x) = P(x)^2.\]اگر $P(x)^2$ را بسط دهیم، همان توزیع آشنا را میگیریم:
\[\begin{aligned} R(x) = x^2 + 2x^3 + 3x^4 + 4x^5 + 5x^6 + 6x^7 \\\\ + 5x^8 + 4x^9 + 3x^{10} + 2x^{11} + x^{12}. \end{aligned}\]ضرایب این چندجملهای دقیقاً همان دنبالهای است که پیشتر دیدیم:
\[1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1.\]گام چهارم: بازنویسی پرسش اصلی با زبان چندجملهای
حالا میتوانیم پرسش «تاسهای غیراستاندارد» را به زبانی دقیقتر و شفافتر بازنویسی کنیم:
آیا میتوان دو چندجملهای $A(x)$ و $B(x)$ با ضرایب صحیحِ مثبت پیدا کرد
که مجموع ضرایب هر کدام برابر ۶ باشد
(چون هر تاس ۶ وجه دارد)،
و حاصلضرب آنها دقیقاً برابر چندجملهای $R(x)$ باشد؟
یعنی:
\[\begin{aligned} A(x)\,B(x) = P(x)^2 = x^2 + 2x^3 + 3x^4 + \\\\ \cdots + 3x^{10} + 2x^{11} + x^{12}, \end{aligned}\]بهعبارت دیگر باید $R(x)$ را تجزیه کنیم.
تجزیهٔ چندجملهای مجموع دو تاس
برای نزدیکشدن به جواب، لازم است خودِ $P(x)$ را بهصورت ضرب چند عامل سادهتر بنویسیم.
گام اول: سادهنویسی $P(x)$ با استفاده از دنبالهٔ هندسی
چندجملهای $P(x)$ را میتوانیم اینگونه ببینیم:
\[\begin{aligned} P(x) = x + x^2 + x^3 + x^4 + x^5 + x^6 \\\\ = x(1 + x + x^2 + x^3 + x^4 + x^5). \end{aligned}\]عبارت داخل پرانتز یک دنبالهٔ هندسی است:
\[1 + x + x^2 + x^3 + x^4 + x^5 = \frac{1 - x^6}{1 - x}.\]پس:
\[P(x) = x \cdot \frac{1 - x^6}{1 - x}.\]حالا $1 - x^6$ را تجزیه میکنیم. میدانیم:
\[1 - x^6 = (1 - x^3)(1 + x^3).\]و هر کدام را باز هم میتوان تجزیه کرد:
-
برای $1 - x^3$ داریم:
\[1 - x^3 = (1 - x)(1 + x + x^2),\] -
و برای $1 + x^3$:
\[1 + x^3 = (1 + x)(1 - x + x^2).\]
اینها را در هم ضرب میکنیم:
\[1 - x^6 = (1 - x)(1 + x + x^2)(1 + x)(1 - x + x^2).\]حالا $P(x)$ را یادآوری کنیم:
\[\begin{aligned} P(x) = x \cdot \frac{1 - x^6}{1 - x} = x \cdot \frac{(1 - x)(1 + x + x^2)(1 + x)(1 - x + x^2)}{1 - x}. \end{aligned}\]عامل $(1 - x)$ در صورت و مخرج ساده میشود و میماند:
\[P(x) = x(1 + x)(1 + x + x^2)(1 - x + x^2).\]این یک تجزیهٔ بسیار مهم است: چندجملهای یک تاس استاندارد به چهار عاملِ نسبتاً ساده شکسته شد.
گام دوم: تجزیهٔ $R(x) = P(x)^2$
اکنون:
\[R(x) = P(x)^2 = \bigl[x(1 + x)(1 + x + x^2)(1 - x + x^2)\bigr]^2.\]بنابراین:
\[R(x) = x^2 (1 + x)^2 (1 + x + x^2)^2 (1 - x + x^2)^2.\]این تجزیه چیزی شبیه این میگوید:
توزیع مجموع دو تاس استاندارد را میتوان به چهار «عامل» شکاند،
که هر کدام دو بار (به توان ۲) ظاهر شدهاند.
گام سوم: ترجمهٔ دوباره به زبان تاسها
حالا میتوانیم پرسش اصلی را بهزبان این عوامل بنویسیم:
ما بهدنبال دو چندجملهای $A(x)$ و $B(x)$ هستیم بهطوریکه:
\[A(x) \cdot B(x) = x^2 (1 + x)^2 (1 + x + x^2)^2 (1 - x + x^2)^2\]و:
- ضرایب $A(x)$ و $B(x)$ اعداد صحیحِ مثبت باشند؛
- مجموع ضرایب $A(x)$ برابر ۶ (۶ وجه تاس اول)،
- و مجموع ضرایب $B(x)$ نیز برابر ۶ (۶ وجه تاس دوم) باشد.
از آنجا که هر عامل به توان ۲ رسیده است، برای هر کدام از چهار عاملِ زیر:
\[x, \quad (1 + x), \quad (1 + x + x^2), \quad (1 - x + x^2)\]باید تصمیم بگیریم چه «مقداری از توان» را به $A(x)$ و چه مقداری را به $B(x)$ بدهیم:
- مثلاً برای $(1 + x)^2$ میتوانیم:
- کلِ $(1 + x)^2$ را به $A(x)$ بدهیم و هیچ به $B(x)$،
- یا یک $(1 + x)$ به $A(x)$ و یک $(1 + x)$ به $B(x)$،
- یا برعکس، همه را به $B(x)$.
به این ترتیب، مسئله به یک بازی ترکیبیاتیِ مرتبکردن توانها تبدیل میشود:
تمام راههای ممکنِ پخشکردن توانهای این عوامل بین $A(x)$ و $B(x)$ را در نظر میگیریم،
و آنهایی را نگه میداریم که:
- ضرایبشان مثبت باشد،
- مجموع ضرایبشان ۶ باشد،
- و در نهایت واقعاً یک چندجملهای «تاسی» معقول بسازند.
در ادامه خواهیم دید که این کار—با وجود ظاهر فنیاش— منجر به یک نتیجهٔ بسیار زیبا و شگفتآور میشود:
به غیر از تاسهای استاندارد، فقط یک زوج تاس غیراستاندارد که چنین توزیع مجموعی را تولید میکند؛ تاسی که در ادبیات به نام Sicherman dice مشهور است.
شرط کلیدی: مجموع ضرایب باید برابر ۶ باشد
برای هر چندجملهای که نمایانگر یک تاس است، مجموع ضرایب آن باید برابر ۶ باشد؛ چون هر تاس دقیقاً ۶ وجه دارد.
اگر چندجملهای $A(x)$ نمایندهٔ یک تاس باشد، مجموع ضرایب آن برابر است با:
\[A(1).\]بنابراین شرط اصلی ما این است:
\[A(1) = 6, \qquad B(1) = 6.\]نگاهی به عوامل تشکیلدهندهٔ $P(x)$
یادآوری کنیم که $R(x)$ (چندجملهای مجموع دو تاس استاندارد) را اینگونه تجزیه کردیم:
\[R(x) = x^2 (1 + x)^2 (1 + x + x^2)^2 (1 - x + x^2)^2.\]چهار «عامل» مهم در این تجزیه وجود دارد:
- $x$
- $1 + x$
- $1 + x + x^2$
- $1 - x + x^2$
برای اینکه بدانیم هر کدام چه سهمی در مجموع ضرایب دارند، کافی است $x=1$ را در آنها قرار دهیم:
-
برای $x$:
\(x \big|_{x=1} = 1\) -
برای $x+1$:
\((1 + x)\big|_{x=1} = 2\) -
برای $1 + x + x^2$:
\((1 + x + x^2)\big|_{x=1} = 3\) -
برای $1 - x + x^2$:
\((1 - x + x^2)\big|_{x=1} = 1\)
پس مقادیر هر عامل (در $x=1$) برابر است با:
\[1,\; 2,\; 3,\; 1.\]برای رسیدن به مجموع ۶، باید دقیقا یک ۲ و یک ۳ در هم ضرب شوند. یعنی هر تاس (هم $A(x)$ و هم $B(x)$)
باید دقیقاً یک عامل ۳تایی و یک عامل ۲تایی را داشته باشد.
به بیان دقیقتر:
- هر کدام از دو چندجملهای باید دقیقاً یک نسخه از عامل $1 + x + x^2$ (که مقدار ۳ دارد) داشته باشد،
- دقیقاً یک نسخه از عامل $1 + x$ (که مقدار ۲ دارد).
یک مشاهدهی دیگر: نمیتوان هر دو عامل $x$ را به یکی از تاسها اختصاص داد
اگر هر دو نسخهٔ $x$ به $A(x)$ داده شود، در $B(x)$ قطعا یک جمله ضریب ثابت (ضریب $x^0$) ظاهر میشود. این یعنی عدد ۰ روی تاس ظاهر میشود. اما ما تنها اجازه داریم اعداد صحیحِ مثبت روی وجههای تاس بنویسیم؛ نه صفر، نه مقدار منفی. بنابراین:
هر دو چندجملهای $A(x)$ و $B(x)$ باید دقیقاً یک نسخه از $x$ داشته باشند.
اگر عامل $1 - x + x^2$ را نیز بهصورت مساوی بین دو تاس تقسیم کنیم به همان تاسهای استاندارد برمیگردیم. پس به یکی از تاسها هر دوی این عامل را میدهیم و به دیگری نمیدهیم. پس برای ساختن تاسهای غیراستاندارد باید:
- عاملِ $1 - x + x^2$: نامتقارن تقسیم شود.
یعنی یکی از تاسها هر دو نسخه را بگیرد
و دیگری هیچ نسخهای از این عامل نداشته باشد. - بقیهی عوامل: بین دو تاس نصف شود (هر کدام یک نسخه).
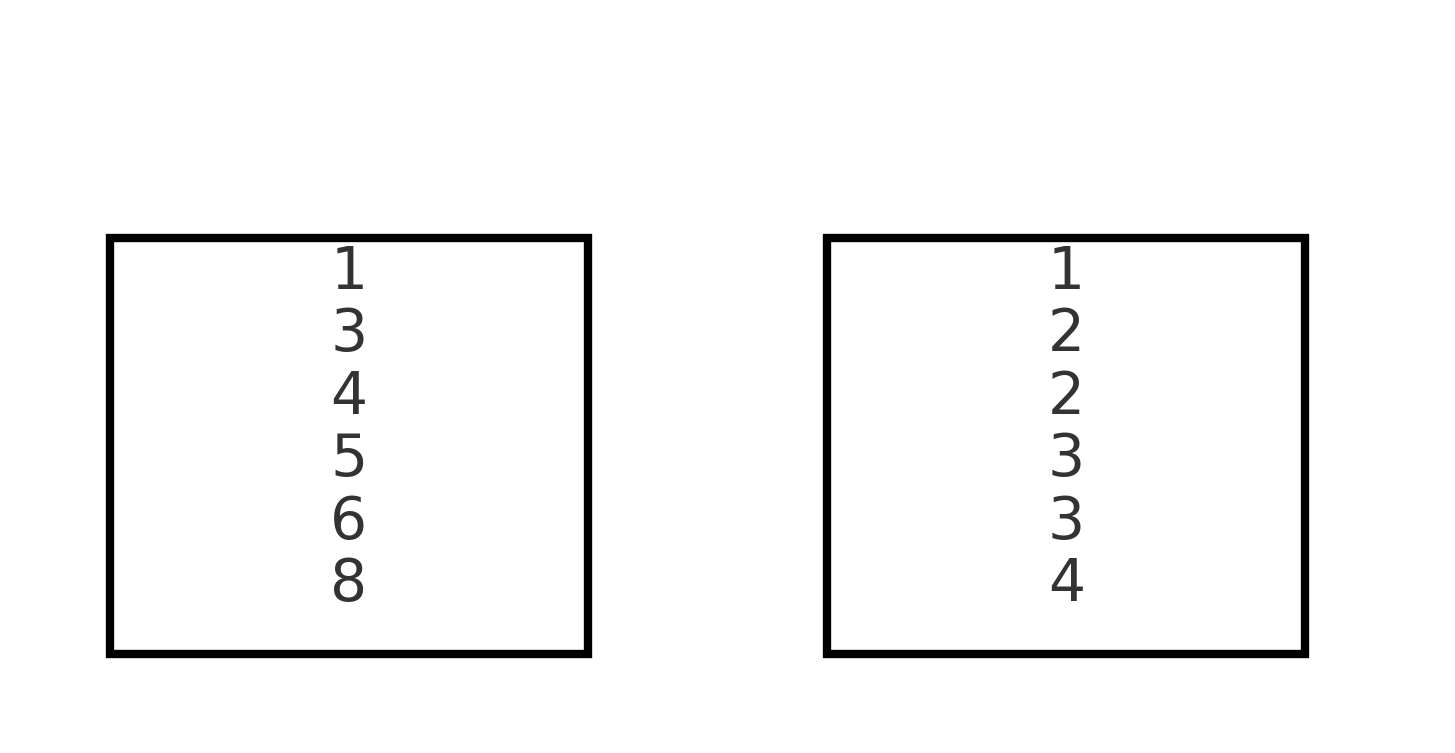
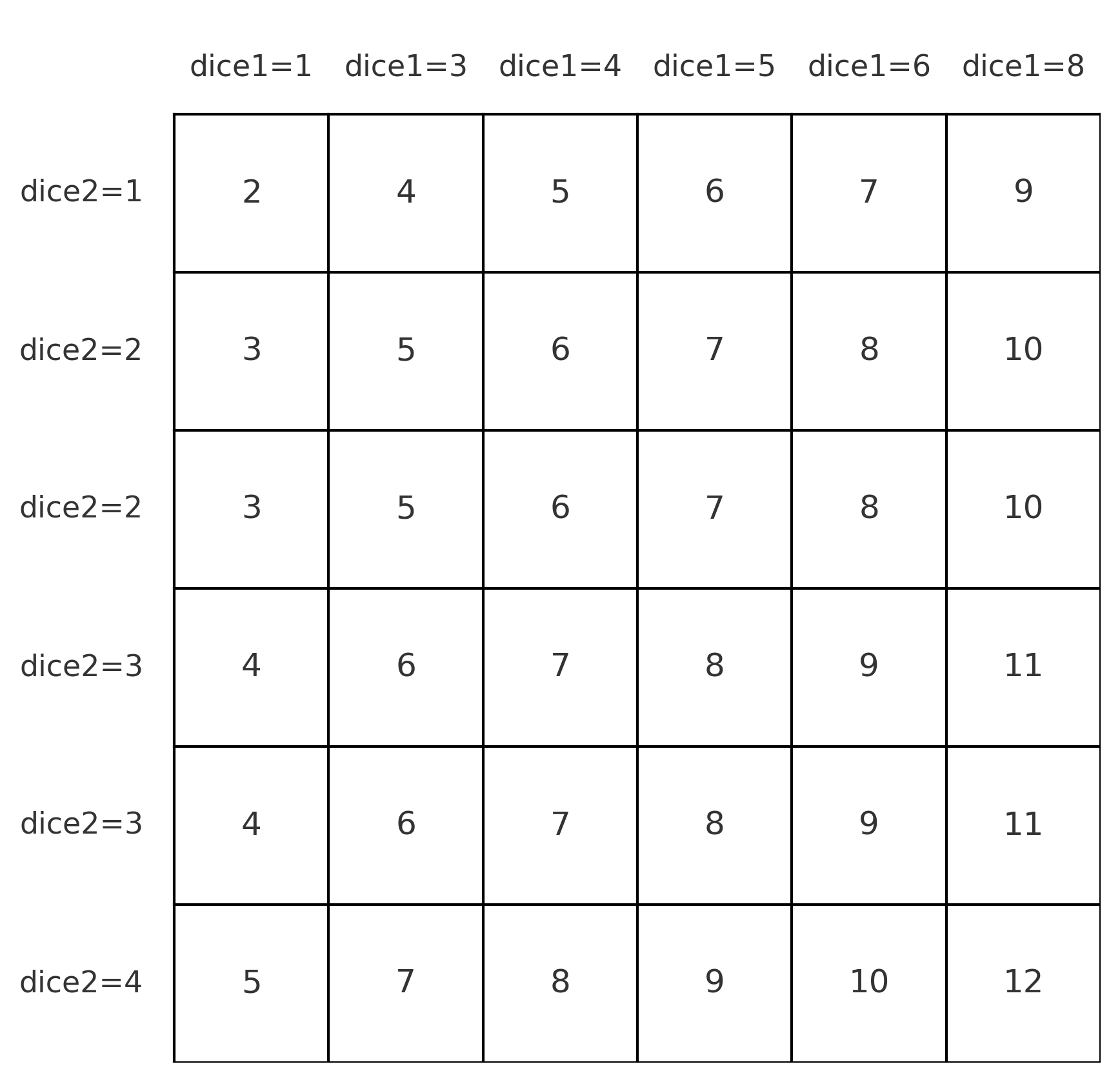
این یعنی تاس اول دارای وجوه:
\[\{1,\ 3,\ 4,\ 5,\ 6,\ 8\}.\]برای $B(x)$ داریم:
\[\begin{aligned} B(x) = x(1+x)(1+x+x^2) \\\\ = x + 2x^2 + 2x^3 + x^4. \end{aligned}\]این یعنی تاس دوم دارای وجوه:
\[\{1,\ 2,\ 2,\ 3,\ 3,\ 4\}.\]اگر این دو تاس را بیندازید و فقط به «مجموع» نگاه کنید، هیچ آزمایشی نمیتواند آنها را از دو تاس استاندارد تشخیص دهد؛ هرچند ظاهرشان کاملاً متفاوت است.