تقارن در بازیها: نخستین نگاه
تقارن فقط برای زیباتر کردن شکلها نیست؛ در بسیاری از بازیها و مسئلههای استراتژیک، تقارن تعیین میکند چه کسی برنده است.
مسئلهٔ میز دایرهای و سکهها
یک میز دایرهای به شعاع ۱۰۰ در نظر بگیرید. دو بازیکن داریم که بهنوبت روی این میز سکههایی با شعاع ۱ قرار میدهند. قواعد ساده است:
- سکه نباید از لبهٔ میز بیرون بزند،
- سکهها نباید روی هم قرار بگیرند،
- و بازیکنی که نتواند سکهای بگذارد، بازنده است.
کدام بازیکن میتواند استراتژیِ برد داشته باشد؟ نفر اول یا دوم؟
این بازی از بیرون شبیه همان بازیهای کلاسیک «چیدن آهنرباها» یا «گذاشتن مهرهها روی صفحه بدون تماس» است؛ اما قلب مسئله جای دیگری است: در تقارنِ کاملِ میز و فضا. پیشنهاد میکنم پیش از خواندن ادامهی این نوشته کمی به این پرسش فکر کنید.
ایدهٔ تقارن مرکزی
گام اول در حل این مسئله این است که خودِ میز را جدی بگیریم: میز ما یک دایره است، و دایره از متقارنترین شکلهای هندسی است. اگر مرکز دایره را $O$ بنامیم، هر نقطهای روی میز — مثلاً $P$ — یک «همتای متقارن» نسبت به مرکز دارد که آن را $P’$ مینامیم:
- نقطهٔ $P’$ آنسوی مرکز قرار دارد،
- بهطوریکه $O$ وسطِ پارهخطِ $PP’$ است،
- و فاصلهٔ $P$ تا $O$ با فاصلهٔ $P’$ تا $O$ برابر است.
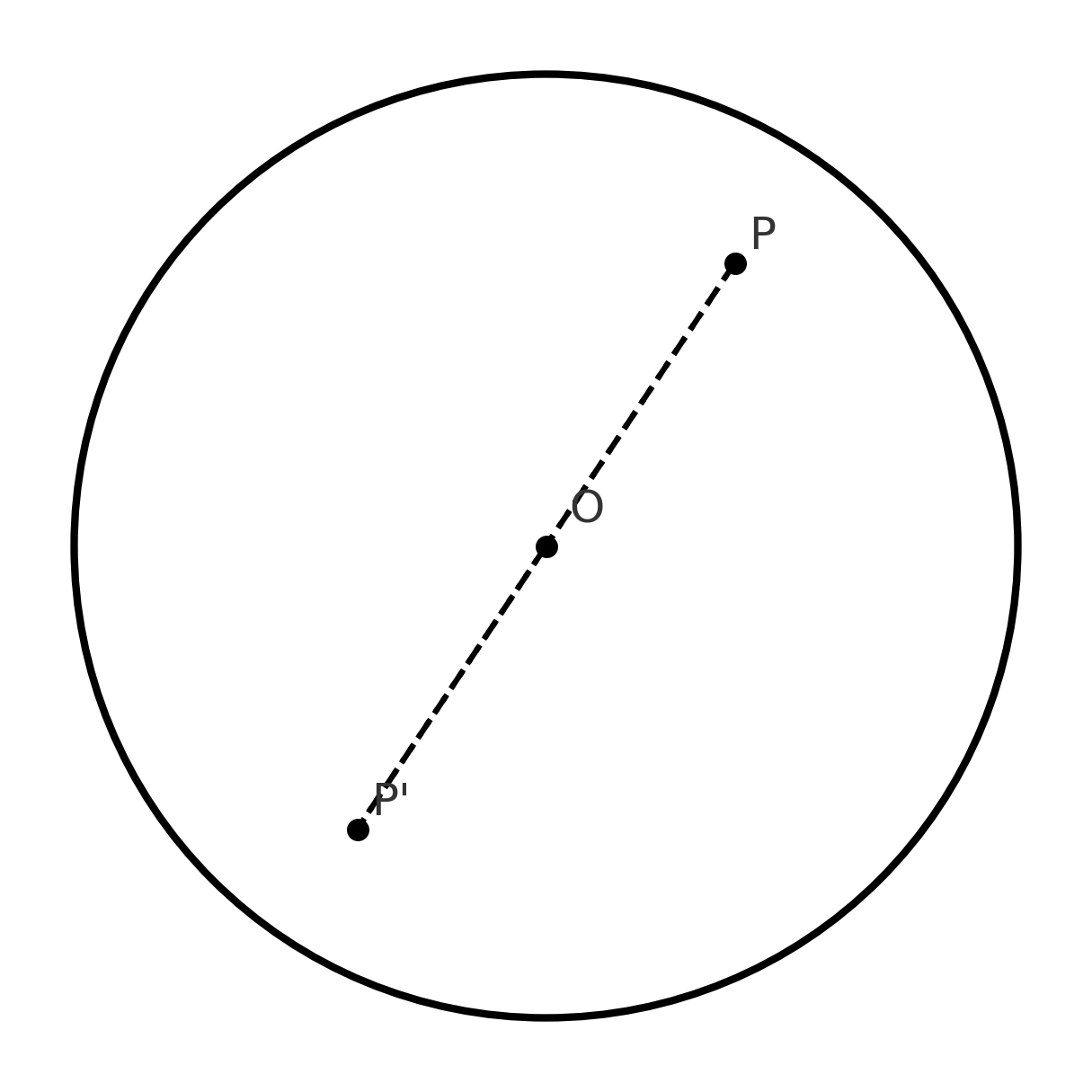
این مشاهدهٔ ساده به ما اجازه میدهد بهجای فکر کردن به جایگذاریِ تکتک سکهها، به سکهها بهصورت جفتهای متقارن فکر کنیم:
هر جایی که بتوان یک سکه گذاشت، در نقطهٔ قرینهاش (نسبت به مرکز) هم ـ اگر سکهای نباشد ـ میتوان سکهای دیگر گذاشت.

در بخش بعدی از همین ایده استفاده میکنیم تا یک استراتژیِ برد برای یکی از بازیکنان بسازیم:
استراتژیای که بر پایهٔ حرکت اولِ درست و سپس تقلیدِ متقارن بنا شده است.
استراتژی برنده
اکنون که میدانیم هر نقطه روی میز یک نقطهٔ قرینه نسبت به مرکز دارد، میتوانیم از این تقارن برای ساختن یک استراتژیِ برد استفاده کنیم. کل ایده روی دو گام استوار است:
- حرکت اولِ درست، در مرکز دایره.
- تقلیدِ متقارنِ تمام حرکتهای حریف.
گام اول: سکهٔ اول را کجا بگذاریم؟
بازیکن اول کافی است سکهٔ نخست خود را دقیقاً در مرکز میز قرار دهد. این نقطه نسبت به خودش قرینه است؛ یعنی قرینهٔ مرکزیِ مرکز، دوباره همان مرکز است.
گام دوم: تقلید متقارن
فرض کنید بازیکن دوم سکهای را در نقطهای مانند $P$ روی میز قرار میدهد. بازیکن اول در پاسخ، سکهٔ خود را در نقطهٔ قرینهٔ $P$ نسبت به مرکز میز میگذارد؛ یعنی دقیقاً در همان فاصله از مرکز، اما در جهت مقابل. به این ترتیب:
- اگر سکهٔ بازیکن دوم کاملاً داخل میز جا شده است،سکهٔ متقارنِ بازیکن اول نیز حتماً کاملاً داخل میز جا میشود؛ چون قرینهٔ مرکزی، دایره را به خودش میبرد.
- اگر سکهٔ بازیکن دوم با هیچ سکهٔ دیگری برخورد نداشته است، سکهٔ متقارنِ بازیکن اول نیز با هیچ سکهای برخورد نخواهد داشت؛ چون فاصلهها نسبت به مرکز حفظ میشوند و قرینهبودن، این ساختار را نگه میدارد.
پس هر حرکت مجازِ بازیکن دوم، یک حرکت مجازِ متقارن برای بازیکن اول ایجاد میکند.
نتیجه: چرا بازیکن اول میبَرد؟
این استراتژی یک پیام ساده دارد: تا زمانی که بازیکن دوم بتواند سکهای روی میز بگذارد، بازیکن اول نیز میتواند سکهای در نقطهٔ تقارنِ آن بگذارد. بنابراین اگر در نهایت میز آنقدر پر شود که بازیکن دوم دیگر نتواند سکهای بگذارد، یعنی:
- او آخرین حرکت را انجام نداده است،
- و هر حرکتی که توانسته انجام دهد،
بازیکن اول بلافاصله حرکتی متقارن در برابرش داشته است.
پس لحظهای که بازیکن دوم به بنبست میرسد، بازیکن اول پیش از او آخرین سکهٔ ممکن را روی میز گذاشته است؛ یعنی بازیکن اول برنده است.
همهٔ این استدلال تنها بر یک چیز تکیه داشت: اینکه باعث شویم ساختار بازی نسبت به مرکز متقارن بماند، و بازیکن اول با یک حرکت ابتداییِ هوشمندانه (گذاشتن سکه در مرکز) کنترل این تقارن را در دست بگیرد.
