مسئلهٔ چراغ‌ها و کلیدها

ساختمان روشنايی تعداد زيادی چراغ و كليد دارد. هر كليد به بعضی از چراغ‌ها متصل است و با زدن آن وضعيت همه آن چراغ‌ها تغيير مي‌كند. می‌دانيم هر چراغ دست‌كم به یک كليد متصل است. نشان دهيد اگر در ابتدا همه چراغ‌ها خاموش باشند می‌توان با زدن بعضی از كليدها به حالتی رسيد كه بيش از نيمی از چراغ‌ها روشن باشد. (ایران ۱۳۸۸)

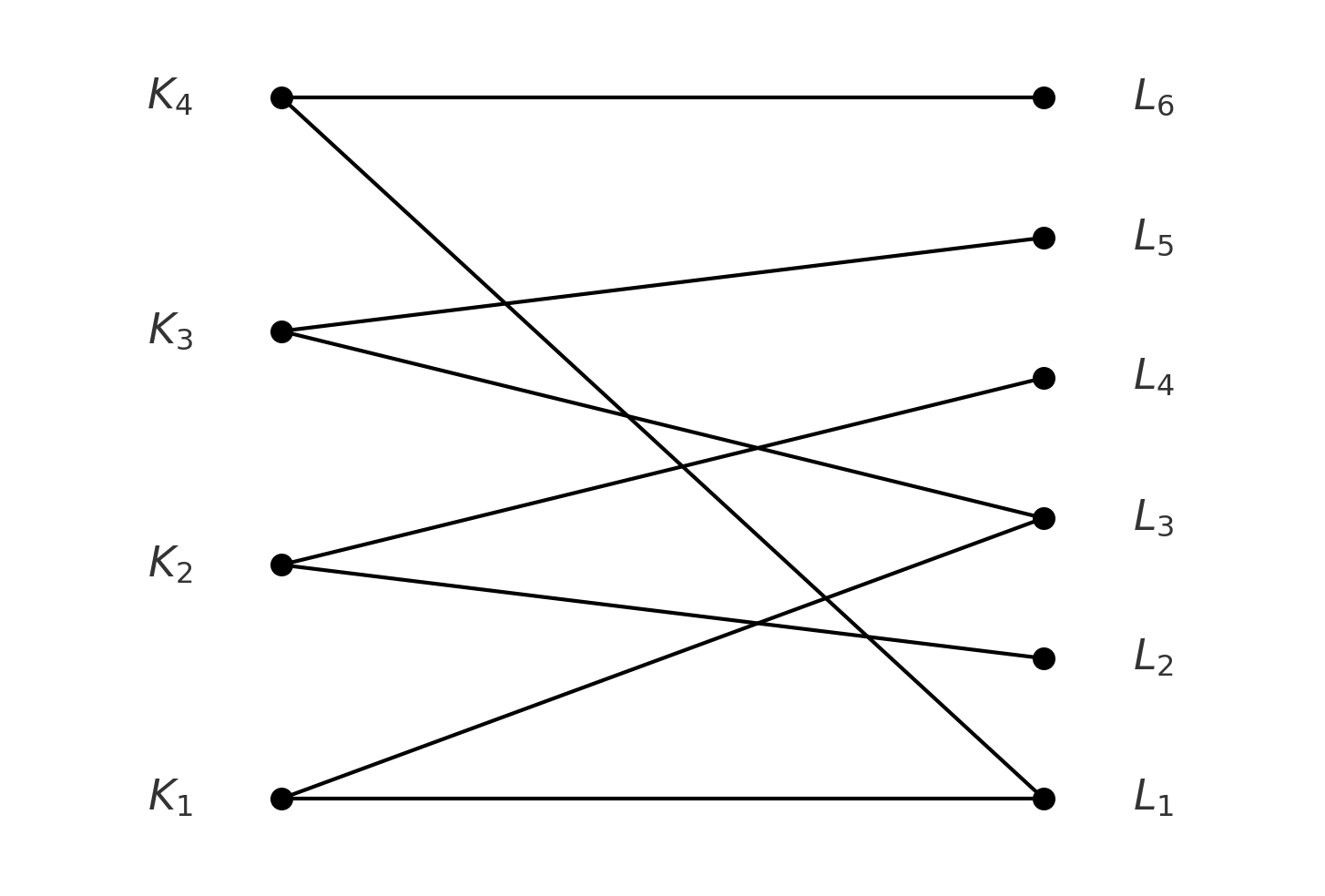
مدل‌سازی مسئله با یک گراف دوبخشی

چرا بازنویسی مسئله آن را قابل‌حل‌تر می‌کند؟

مسئلهٔ چراغ‌ها و کلیدها در ظاهر یک پرسش سادهٔ «روشن و خاموش کردن» است؛ اما اگر بخواهیم آن را تحلیل کنیم، زنجیره‌ای از وابستگی‌ها و اثرگذاری‌های متقاطع پیش رویمان قرار می‌گیرد:
هر کلید تعدادی چراغ را تغییر می‌دهد، و هر چراغ زیرمجموعه‌ای از کلیدها را تحت تأثیر قرار می‌دهد.
برای دیدن ساختار واقعی مسئله، بهتر است آن را به زبان دیگری بازنویسی کنیم—زبانی که ارتباط‌ها در آن آشکارتر باشند.

بهترین ابزار برای این کار، گراف دوبخشی است.

---

گام اول: تبدیل کلیدها و چراغ‌ها به دو دستهٔ گره

دو دستهٔ مجزا تعریف می‌کنیم:

• دستهٔ اول: کلیدها ($K_i$)
• دستهٔ دوم: چراغ‌ها ($L_j$)

بین یک کلید و یک چراغ یک یال قرار می‌دهیم اگر و تنها اگر زدن آن کلید وضعیت آن چراغ را تغییر دهد. در این مدل، هیچ یالی بین دو کلید یا دو چراغ وجود ندارد؛ پس نمودار به‌صورت طبیعی یک گراف دوبخشی می‌شود.

---

گام دوم: چرا این مدل مفید است؟

در این مدل‌سازی:

• هر کلید معادل یک گره است که با چند چراغ ارتباط دارد.
• هر چراغ نیز معادل یک گره است که به کلیدهای متصل به آن وابسته است.
• «زدن کلید» دقیقاً یعنی وارونه کردن وضعیت همهٔ گره‌های سمت چراغ که با آن یال دارند.

به‌این‌ترتیب، رفتار مسئله دیگر درگیر توصیف لفظی نیست؛ بلکه به یک ساختار منظم و قابل‌بحث تبدیل شده است. این همان معنای واقعی recasting است: بازنویسی مسئله در قالبی که رفتار آن را آشکارتر و قابل‌دسترس‌تر کند.
اکنون که ساختار مسئله را روشن کردیم، دو راه‌حل کاملا متفاوت برای حل این مسئله ارائه می‌کنیم. پیشنهاد می‌کنیم پیش از خواندن راه‌حل‌ها خودتان چند ساعت به این پرسش فکر کنید.

---

روش اول: استقرا بر تعداد کلیدها

بگذارید تعداد کلیدها را $m$ و تعداد چراغ‌ها را $n$ بنامیم. می‌خواهیم نشان دهیم برای هر ساختمانی با این ویژگی‌ها، می‌توان با انتخاب بعضی از کلیدها به حالتی رسید که بیش از نیمی از چراغ‌ها روشن باشند. ایده این است که روی تعداد کلیدها استقرا بزنیم.

---

پایهٔ استقرا: یک کلید

اگر فقط یک کلید وجود داشته باشد ($m = 1$)، از فرض مسئله می‌دانیم که «هر چراغ دست‌کم به یک کلید وصل است»؛ پس همین یک کلید به همهٔ چراغ‌ها وصل است.

در ابتدا همهٔ چراغ‌ها خاموش‌اند. اگر این کلید را یک‌بار بزنیم، وضعیت همهٔ چراغ‌ها عوض می‌شود و همه روشن می‌شوند.
بنابراین نه‌تنها بیش از نیمی، بلکه تمام چراغ‌ها روشن می‌شوند. پس حکم برای $m=1$ درست است.

---

ایدهٔ استقرا: کوچک‌کردن مسئله

حال فرض کنید حکم برای هر ساختمانی با کمتر از $m$ کلید درست باشد (فرض استقرا)، و حالا ساختمانی با $m$ کلید داریم.

می‌خواهیم از یک ساختمان با $m$ کلید، یک ساختمان کوچک‌تر بسازیم که هنوز مسئله در آن معتبر است، و بعد از جواب آن، جواب این یکی را بازسازی کنیم.

ایدهٔ طبیعی این است که:

1. یک کلید انتخاب کنیم (مثلاً $K$)،
2. این کلید و تمام از چراغ‌های مرتبط با آن را «کنار بگذاریم»،
3. روی بقیهٔ گراف از فرض استقرا استفاده کنیم.

برای این کار، دقت کنیم که $K$ دست‌کم به یک چراغ وصل است
(اگر کلیدی به هیچ چراغی وصل نباشد، کاملاً بی‌اثر است و می‌توانیم از ابتدا او را نادیده بگیریم).

---

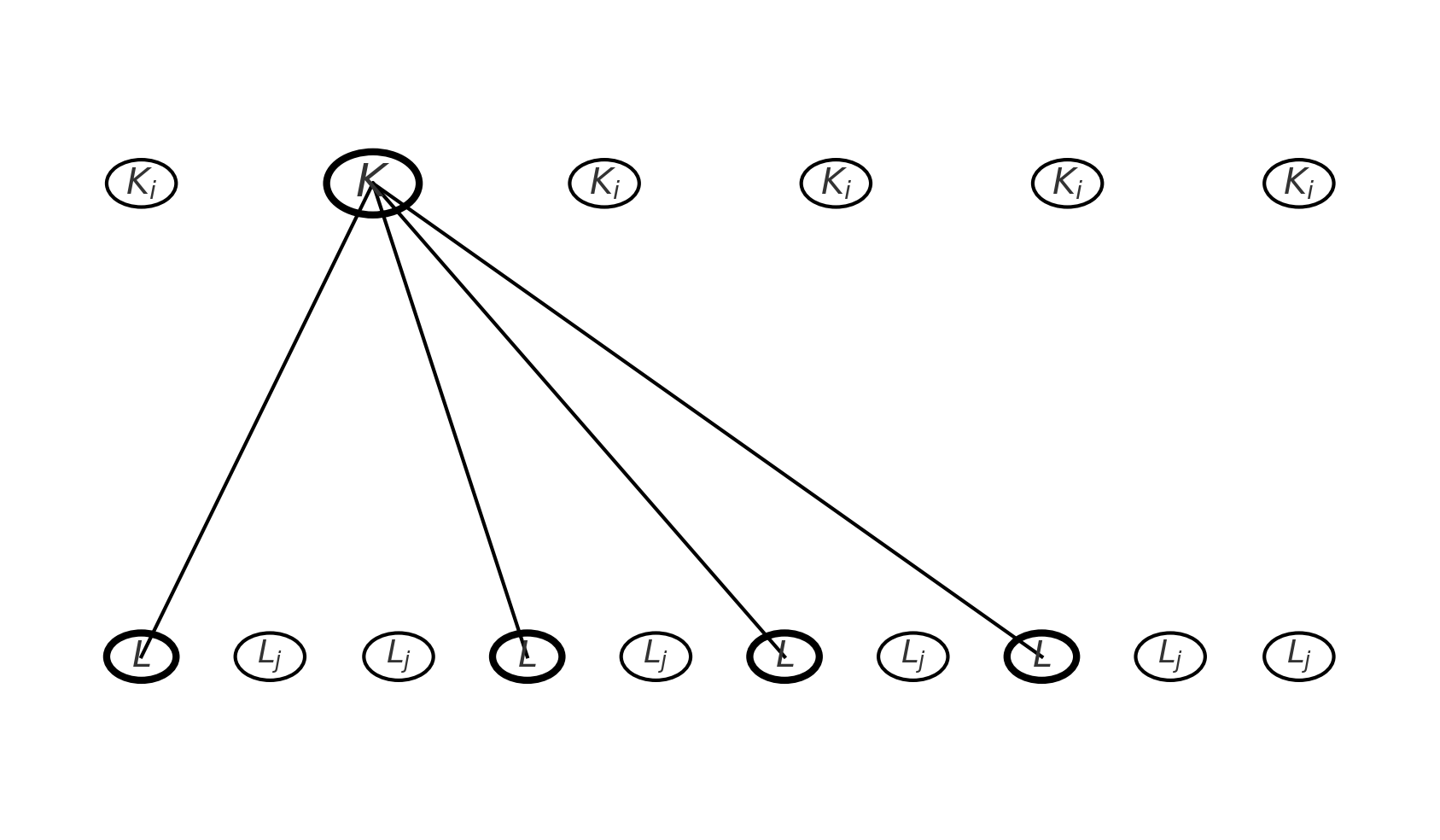
گام اول: حذف یک کلید و چراغ‌های متصل به آن

کلیدی را انتخاب می‌کنیم، آن را $K$ می‌نامیم، و مجموعهٔ چراغ‌هایی را که به آن وصل‌اند با $N(K)$ نشان می‌دهیم. حالا:

• کلید $K$ را حذف می‌کنیم،
• همهٔ چراغ‌های متصل به $K$ یعنی تمام اعضای $N(K)$ را نیز حذف می‌کنیم.

چیزی که باقی می‌ماند یک زیرگراف است با:

• تعدادی کلید (حداکثر $m-1$ تا)،
• و تعدادی چراغ (بگویید $n’$ تا) که هیچ‌کدام از آن‌ها به $K$ وصل نبودند.

نکتهٔ مهم:

• چراغ‌هایی که باقی مانده‌اند، همان‌هایی هستند که اصلاً به $K$ وصل نبودند،
• و از ابتدا هر چراغ دست‌کم به یک کلید وصل بود،
• بنابراین پس از حذف $K$، این چراغ‌ها همچنان دست‌کم یک کلید مجاور دارند.

پس فرض مسئله (هر چراغ دست‌کم به یک کلید وصل است) برای این گراف کوچک‌شده نیز برقرار است.

---

گام دوم: استفاده از فرض استقرا روی گراف کوچک‌تر

اکنون در این گراف کوچک‌تر:

• تعداد کلیدها کمتر از $m$ است،
• تعداد چراغ‌ها $n’$ است،
• و شرایط مسئله برقرار است.

بنابراین طبق فرض استقرا، می‌توان برخی از کلیدهای باقی‌مانده را طوری زد که بیش از نیمی از این $n’$ چراغ روشن شوند.

یعنی می‌توان زیرمجموعه‌ای از کلیدها $S$ (بدون $K$) را انتخاب کرد به‌طوری که اگر فقط همین کلیدها زده شوند، در گراف کوچک‌شده تعداد چراغ‌های روشن بیشتر از $\frac{n’}{2}$ باشد.

حالا می‌خواهیم همین انتخاب $S$ را برای کل ساختمان (با همهٔ چراغ‌ها و با خودِ $K$) به‌کار ببریم.

---

گام سوم: بازگشت به گراف اصلی و تصمیم دربارهٔ کلید $K$

وقتی در گراف اولیه فقط کلیدهای مجموعهٔ $S$ را می‌زنیم:

• چراغ‌های خارج از $N(K)$ (یعنی چراغ‌هایی که حذفشان کرده بودیم)
  دقیقاً همان رفتاری را دارند که در گراف کوچک‌شده داشتند؛
  پس بیش از $n’/2$ عدد از آن‌ها روشن‌اند.

• چراغ‌های درون $N(K)$ ممکن است روشن یا خاموش باشند؛
  بسته به این‌که چند کلید دیگر (از مجموعهٔ $S$) به آن‌ها وصل است.

اکنون فقط یک انتخاب اضافه داریم:
کلید $K$ را بزنیم یا نزنیم.

• اگر $K$ را نزنیم، تعداد چراغ‌های روشن در $N(K)$ را $a$ بنامیم.
• اگر $K$ را بزنیم، وضعیت همهٔ چراغ‌های $N(K)$ وارونه می‌شود؛
  بنابراین تعداد چراغ‌های روشن در این مجموعه برابر $d - a$ می‌شود،
  که $d$ تعداد چراغ‌های متصل به $K$ است (یعنی اندازهٔ $N(K)$).

در هر صورت، میان دو عدد $a$ و $d-a$،
حداقل یکی به‌اندازهٔ حداقل نصف $d$ است:

$$\max(a, d-a) \;\ge\; \frac{d}{2}.$$

پس می‌توانیم یکی از دو حالت را انتخاب کنیم:

• یا $K$ را نزنیم،
• یا $K$ را بزنیم،

به‌گونه‌ای که دست‌کم نیمی از چراغ‌های $N(K)$ روشن باشند.

---

گام چهارم: جمع‌زدن دو نیمه

حالا دو دسته چراغ داریم:

1. چراغ‌هایی که در گراف کوچک‌شده باقی مانده بودند (تعدادشان $n’$ بود)،
   که بیش از $\dfrac{n’}{2}$ عدد از آن‌ها روشن‌اند؛

2. چراغ‌های متصل به $K$ یعنی همان $N(K)$ با اندازهٔ $d$،
   که می‌توانیم طوری انتخاب کنیم (با زدن یا نزدن $K$)
   که دست‌کم $\dfrac{d}{2}$ عدد از آنها روشن باشند.

پس در مجموع، تعداد چراغ‌های روشن بیشتر از:

$$\frac{n'}{2} + \frac{d}{2} = \frac{n' + d}{2} = \frac{n}{2}$$

خواهد بود (چون $n = n’ + d$).

بنابراین توانستیم زیرمجموعه‌ای از کلیدها (همان $S$، به‌علاوهٔ «زدن یا نزدن» $K$) پیدا کنیم که در گراف اصلی، بیش از نیمی از چراغ‌ها را روشن می‌کند. این دقیقاً همان چیزی است که باید ثابت می‌کردیم.

به این ترتیب، استقرا کامل می‌شود:
اگر حکم برای همهٔ ساختمان‌هایی با کمتر از $m$ کلید درست باشد، برای ساختمان با $m$ کلید هم درست است. و چون پایهٔ استقرا ($m=1$) را دیدیم، نتیجه می‌گیریم که برای هر تعداد کلید و چراغ با شرایط مسئله، می‌توان بیش از نیمی از چراغ‌ها را روشن کرد.

---

روش دوم: اصل میانگین

ایده‌ای ساده، اما درخشان

پیش از آن‌که وارد حل مسئله شویم، یک مشاهدهٔ ابتدایی اما بسیار قدرتمند را مرور می‌کنیم—اصل میانگین.

فرض کنید چند عدد داشته باشیم و میانگین آن‌ها برابر $M$ باشد. اصل میانگین می‌گوید:

دست‌کم یکی از این عددها بزرگ‌تر یا مساویِ $M$ است.

چرا؟ اگر همهٔ عددها ($n$ عدد) کمتر از میانگین بودند، مجموعشان نیز کمتر از $n \times M$ می‌شد—که تناقض است. پس حتماً یک عدد وجود دارد که میانگین را «تحقق» می‌بخشد یا از آن بالاتر می‌رود.

این اصل ساده در نگاه اول بدیهی به‌نظر می‌رسد، اما کاربردهای بسیار عمیقی در ترکیبیات، نظریهٔ گراف، احتمال و حتی آنالیز دارد.
در مسئلهٔ چراغ‌ها و کلیدها، این اصل به شکلی زیبا به ما می‌گوید چگونه بدون ساختن راه‌حل، می‌توان وجود راه‌حل را تضمین کرد.

---

نگاه اول: به‌جای پیدا کردن یک حالت، همهٔ حالت‌ها را ببینیم

در صورت مسئله از ما خواسته شده است مجموعه‌ای از کلیدها را پیدا کنیم که در آن حالت، بیش از نیمی از چراغ‌ها روشن باشند.

نگاه طبیعی این است که:

• سعی کنیم «یک» زیرمجموعهٔ خوب از کلیدها را حدس بزنیم؛
• اما یک راه دیگر این است که به‌جای تمرکز روی یک حالت،
  تمام حالت‌های ممکن را یک‌جا در نظر بگیریم
  و از اصل میانگین استفاده کنیم.

هر کلید دو وضعیت دارد: یا آن را می‌زنیم، یا نمی‌زنیم.
اگر تعداد کلیدها را $m$ بنامیم، در مجموع

$$2^m$$

حالت مختلف برای زدن/نزدن کلیدها وجود دارد (هر حالت برابر است با انتخاب یک زیرمجموعه از مجموعهٔ کلیدها). این حالت‌ها را می‌توانیم به‌صورت زیر نام‌گذاری کنیم:

$$S_1, S_2, \dots, S_{2^m},$$

که در آن $S_k$ نشان‌دهندهٔ «زیرمجموعهٔ $k$ام از کلیدها» است (یعنی کدام کلیدها زده شده‌اند و کدام نه).

---

ساخت یک جدول بزرگ از تمام حالات

حالا به جای این‌که هر حالت را جدا جدا تحلیل کنیم، یک جدول دوبعدی می‌سازیم که:

• هر سطر نمایندهٔ یکی از حالت‌های زدن کلیدها باشد
  (پس در مجموع $2^m$ سطر خواهیم داشت)،

• هر ستون نمایندهٔ یکی از چراغ‌ها باشد
  (اگر تعداد چراغ‌ها $n$ باشد، $n$ ستون داریم).

در هر خانهٔ این جدول یک عدد صفر یا یک می‌نویسیم:

• خانهٔ سطرِ $S_k$ و ستونِ چراغِ $L_j$ برابر ۱ است
  اگر در حالتِ زدنِ کلید‌های $S_k$ چراغِ $L_j$ روشن باشد؛
• و برابر ۰ است
  اگر در حالتِ زدنِ کلید‌های $S_k$ چراغِ $L_j$ خاموش باشد.

به این ترتیب، هر سطر یک ردیف از صفر و یک است که وضعیت چراغ‌ها را در یک حالت مشخص نشان می‌دهد،
و هر ستون نشان می‌دهد که یک چراغ خاص، در چه تعداد از حالت‌ها روشن است.

---

هدف ما در این جدول چیست؟

حالا سؤال اصلی‌مان را می‌توانیم به زبان این جدول بیان کنیم:

آیا سطری در این جدول وجود دارد
که در آن، تعداد ۱ها (چراغ‌های روشن)
بیشتر از $\dfrac{n}{2}$ باشد؟

اگر جواب این سؤال «بله» باشد، یعنی زیرمجموعه‌ای از کلیدها (همان سطر متناظر با آن) داریم که در آن حالت، بیش از نیمی از چراغ‌ها روشن‌اند و مسئله حل می‌شود.

تا این‌جا نگاه ما سطرمحور بوده است: به تعداد ۱ها در هر سطر فکر کرده‌ایم. اما اصل میانگین پیشنهاد می‌کند که گاهی به‌جای نگاه کردن در یک جهت، به جهت دیگر نگاه کنیم. اینجا هم یک حرکت کلیدی این است که:

به‌جای تمرکز روی سطرها،
توجه خود را به ستون‌ها معطوف کنیم.

---

شمارش از دید ستون‌ها: هر چراغ در چند حالت روشن است؟

اکنون به سراغ یک ستون از جدول می‌رویم. ستونِ متناظر با یک چراغ مشخص را $L_i$ بنامیم. می‌خواهیم بدانیم: در میان تمام $2^m$ حالت زدن/نزدن کلیدها، در چند حالت چراغ $L_i$ روشن است؟ فرض کنیم چراغ $L_i$ به طور دقیق به $t$ کلید متصل است (همسایه‌های گرافی آن)، و به بقیهٔ کلیدها وصل نیست.

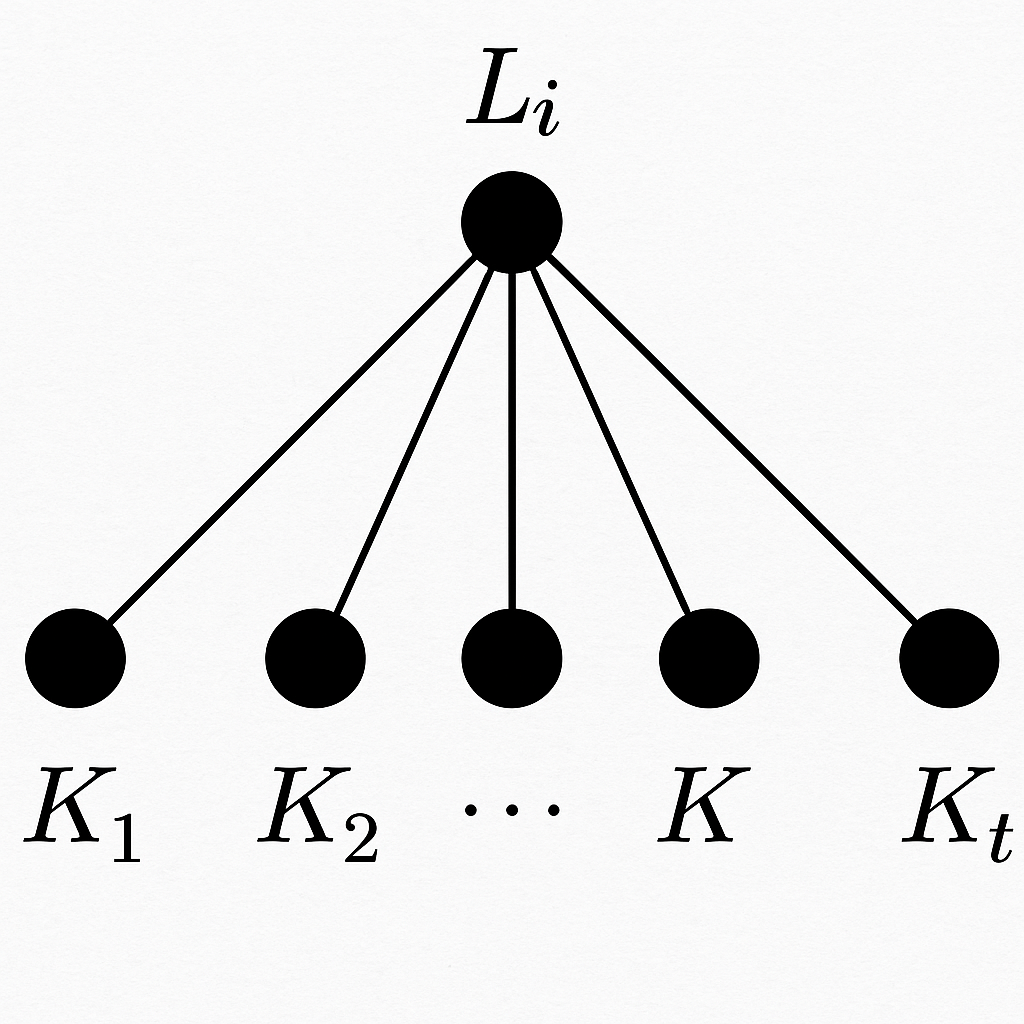
• پس $m - t$ کلید وجود دارند که هیچ تأثیری بر این چراغ ندارند؛
  هر طور بخواهیم آن‌ها را بزنیم یا نزنیم،
  روشن یا خاموش بودن $L_i$ عوض نمی‌شود.

---

یک شمارش هوشمندانه برای همسایه‌های چراغ

حالا تنها باید تعیین کنیم برای $t$ کلید همسایهٔ $L_i$ در چند حالت چراغ روشن می‌شود. یک ایدهٔ بسیار شفاف را به‌کار می‌گیریم:

تمام زیرمجموعه‌های این $t$ کلید را جفت می‌کنیم.

چطور؟

1. همهٔ زیرمجموعه‌های $t-1$ کلید اول را فهرست می‌کنیم.
2. برای هر زیرمجموعهٔ $A$، یک جفت می‌سازیم:
   • زیرمجموعهٔ اول: خودِ $A$
   • زیرمجموعهٔ دوم: $A \cup \set{K_t}$ ($K_t$ کلید آخر است)

در این جفت:

• یکی از زیرمجموعه‌ها زوج تعداد کلید دارد،
• و دیگری فرد تعداد کلید دارد.

و چون روشن یا خاموش بودن $L_i$
فقط به زوج یا فرد بودنِ تعداد کلیدهای زده‌شده بستگی دارد،
در هر جفتِ ساخته‌شده:

• یکی از دو زیرمجموعه چراغ را روشن می‌کند،
• و دیگری چراغ را خاموش می‌کند.

پس:

زیرمجموعه‌های روشن‌کنندهٔ چراغ دقیقاً نصف کل زیرمجموعه‌ها هستند.

تعداد کل زیرمجموعه‌های $t$ کلید برابر $2^t$ است،
پس تعداد زیرمجموعه‌هایی که $L_i$ را روشن می‌کنند برابر است با:

$$2^{t-1}.$$

---

نتیجه‌گیری برای ستونِ چراغ $L_i$

اکنون دو بخش را با هم ترکیب می‌کنیم:

• $2^{m-t}$ انتخاب برای کلیدهای غیرمرتبط،
• $2^{t-1}$ انتخاب روشن‌کننده برای کلیدهای همسایه.

در مجموع:

$$2^{m-t} \times 2^{t-1} = 2^{m-1}$$

حالت وجود دارد که چراغ $L_i$ روشن است.

این یعنی:

هر ستون جدول دقیقاً دارای $2^{m-1}$ عدد «۱» است.

و این سنگ‌بنای اصلی حل با اصل میانگین است.

---

نتیجهٔ مهم: مجموع هر ستون و مجموع کل جدول

پس برای هر چراغ $L_i$، در میان $2^m$ سطر (حالت مختلف زدن کلیدها) دقیقاً در

$$2^{m-1}$$

تا از آن‌ها مقدار ۱ (روشن) در ستونش دیده می‌شود. بنابراین:

• مجموع ستونِ $L_i$ برابر است با $2^{m-1}$،

• و چون $n$ ستون (چراغ) داریم،
  مجموع تمام خانه‌های جدول برابر می‌شود با:

  $$n \cdot 2^{m-1}.$$

از طرف دیگر، اگر تعداد چراغ‌های روشن در سطر $S_k$ را با $R_k$ نشان دهیم،
این مجموع را می‌توانیم این‌طور هم بنویسیم:

$$R_1 + R_2 + \dots + R_{2^m} = n \cdot 2^{m-1}.$$

---

میانگین تعداد چراغ‌های روشن در هر حالت

حالا میانگین تعداد چراغ‌های روشن در یک سطر (یک حالت) برابر است با:

$$M = \frac{R_1 + R_2 + \dots + R_{2^m}}{2^m} = \frac{n \cdot 2^{m-1}}{2^m} = \frac{n}{2}.$$

یعنی اگر همهٔ $2^m$ حالت ممکن زدن کلیدها را در نظر بگیریم،
میانگین تعداد چراغ‌های روشن در این حالت‌ها دقیقاً برابر $\dfrac{n}{2}$ است.

اما یک نکتهٔ ظریف:

• یکی از این سطرها، حالتی است که هیچ کلیدی را نمی‌زنیم.
  در این حالت، همهٔ چراغ‌ها خاموش‌اند،
  پس تعداد چراغ‌های روشن برابر ۰ است
  (و این قطعاً کمتر از $n/2$ است).

طبق اصل میانگین:

اگر میانگینِ مجموعه‌ای از عددها $\dfrac{n}{2}$ باشد
و دست‌کم یک عدد کمتر از میانگین باشد،
حتماً عددی وجود دارد که بیشتر از میانگین باشد.

پس حتماً سطری در جدول وجود دارد که در آن:

$$R_k > \frac{n}{2},$$

یعنی در حالتِ متناظر با این سطر، بیش از نیمی از چراغ‌ها روشن‌اند. این دقیقاً همان چیزی است که مسئله از ما می‌خواست ثابت کنیم.

---

جمع‌بندی شهودی روش میانگین

در نگاه اول ممکن است انتخاب درستِ کلیدها برای روشن‌کردن بیش از نیمی از چراغ‌ها کاری بغرنج و وابسته به ساختار پیچیدهٔ اتصالات به‌نظر برسد. (که البته با استقرا به آن دست‌ یافتیم). اما روش میانگین زاویهٔ نگاه را عوض می‌کند:

• به‌جای این‌که دنبال یک زیرمجموعهٔ مناسب از کلیدها بگردیم،
  همهٔ زیرمجموعه‌ها را یک‌جا در نظر می‌گیریم.

• برای هر چراغ نشان می‌دهیم که در دقیقاً نصف حالت‌های ممکن روشن می‌شود.
  (چون همسایه‌هایش تصمیم را تعیین می‌کنند.)

• بنابراین میانگین تعداد چراغ‌های روشن در میان تمام حالت‌ها
  دقیقاً برابر با نصفِ تعداد چراغ‌ها است.

اما چون حالتی وجود دارد که تعداد چراغ‌های روشن صفر است (هیچ کلیدی را نمی‌زنیم)، میانگین اگر قرار باشد $\dfrac{n}{2}$ شود، حتماً باید حالتی وجود داشته باشد که بالاتر از میانگین باشد.

و این همان است که می‌خواستیم:

حداقل یک انتخاب از کلیدها وجود دارد که بیش از نیمی از چراغ‌ها را روشن می‌کند.

بدون آن‌که حتی یک نمونهٔ مشخص از این انتخاب را پیدا کنیم، فقط با تغییر زاویهٔ نگاه، وجودش را با قطعیت ثابت کردیم.