چرا مجموعِ مکعب‌ها مربعِ مجموع است؟

یکی از زیباترین فرمول‌های مربوط به مجموع‌ها این است:

$$1^3 + 2^3 + 3^3 + \cdots + n^3 = \left(1 + 2 + 3 + \cdots + n\right)^2.$$

این رابطه در نگاه اول کمی غیرمنتظره است: چرا باید جمعِ مکعب‌ها دقیقاً مربعِ یک جمعِ ساده‌تر باشد؟

در این یادداشت، به‌جای محاسبه‌ی جبری،
می‌خواهیم یک نگاه هندسی به این رابطه بیندازیم.

---

بازنویسی مسئله: مربعِ یک مجموع یعنی چه؟

بیایید سمت راست را کمی باز کنیم. اگر بگذاریم:

$$A = 1 + 2 + 3 + \cdots + n,$$

آن‌وقت:

$$A^2 = (1 + 2 + \cdots + n)(1 + 2 + \cdots + n).$$

اما ضربِ دو مجموع یعنی چه؟

یعنی جمعِ همه‌ی حاصل‌ضرب‌های ممکن:

$$A^2 = \sum_{i=1}^n \sum_{j=1}^n ij.$$

این‌جا دقیقاً جایی است که تفسیر هندسی وارد می‌شود.

---

تفسیر هندسی: یک مربعِ بزرگ

مربعِ $A^2$ را می‌توان به‌صورت یک مربعِ بزرگ با ضلعِ $A$ دید.

این مربع را به صورت زیر تقسیم می‌کنیم:

• یک نوار به طولِ $1$،
• بعد یک نوار به طولِ $2$،
• بعد $3$،
• و همین‌طور تا $n$.

هم در جهت افقی، و هم در جهت عمودی.

در نتیجه، مربعِ بزرگ به بلوک‌هایی با مساحت‌های $ij$ تقسیم می‌شود.

هر بلوک، حاصل‌ضربِ یک عدد از سطر و یک عدد از ستون است.

---

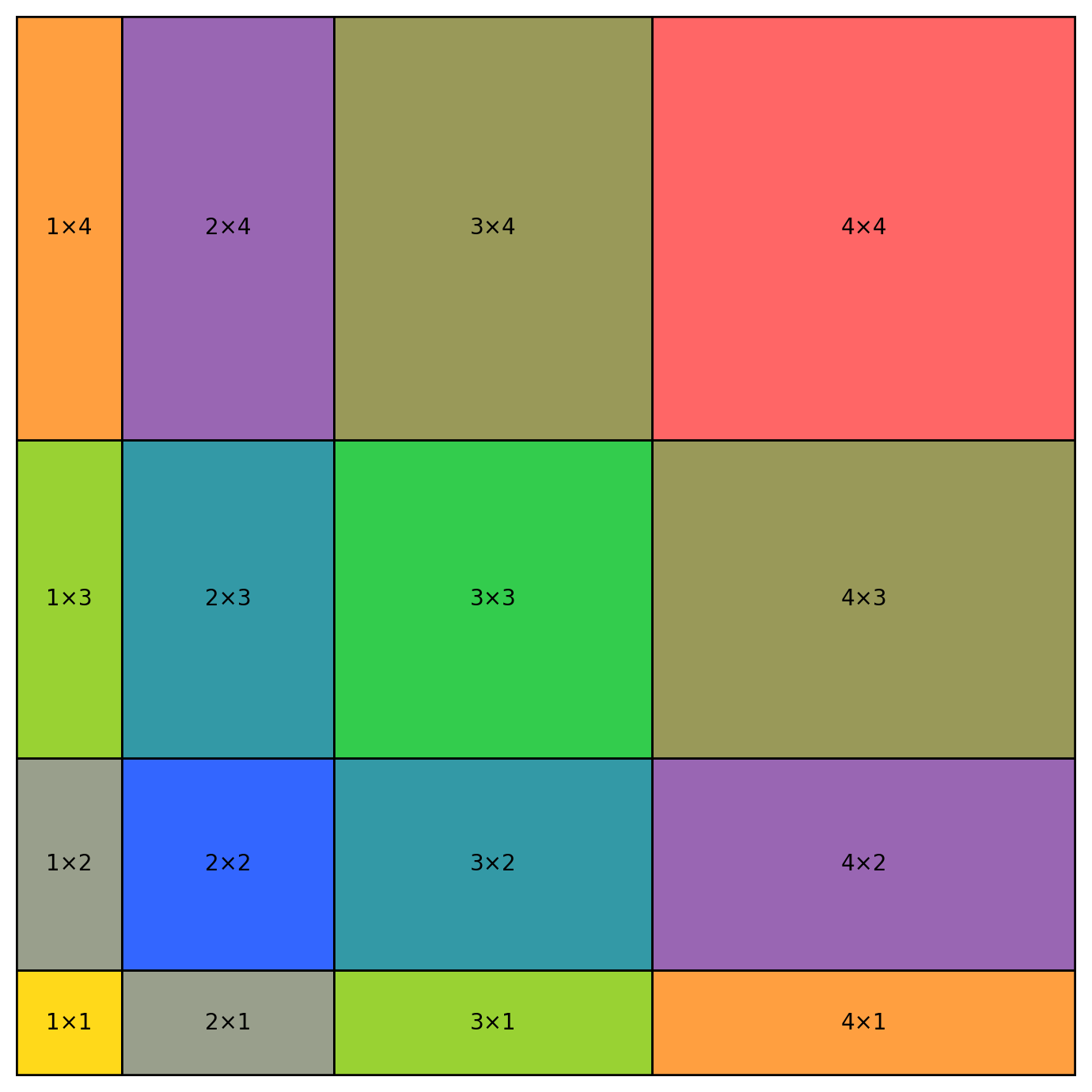
تمرکز روی گوشه: مربع‌های تو در تو

حالا به گوشه‌ی پایین–چپِ شکل نگاه کنید.

اگر فقط نوارهای مربوط به $1,\;2,\;\dots,\;k$ را در هر دو جهت در نظر بگیریم، یک مربع کوچک‌تر با ضلع

$$1+2+\cdots+k$$

خواهیم داشت.

به این ترتیب، درون مربع بزرگ، یک دنباله از مربع‌های تو در تو شکل می‌گیرد:

• مربعِ ضلع $1$،
• بعد مربعِ ضلع $1+2$،
• بعد مربعِ ضلع $1+2+3$،
• و همین‌طور ادامه پیدا می‌کند.

---

هر بار چه چیزی اضافه می‌شود؟

فرض کنید مربعِ مربوط به $k-1$ را ساخته‌ایم. برای رسیدن به مربعِ مربوط به $k$، چه چیزی باید اضافه کنیم؟

دقیقاً یک «لایه‌ی L-شکل»:

• یک نوار افقی با طول $1+2+\cdots+k$ و عرض $k$،
• یک نوار عمودی مشابه،
• که در گوشه روی هم می‌افتند.

این لایه دقیقاً همان چیزی است که مربعِ قبلی را به مربعِ جدید تبدیل می‌کند.

---

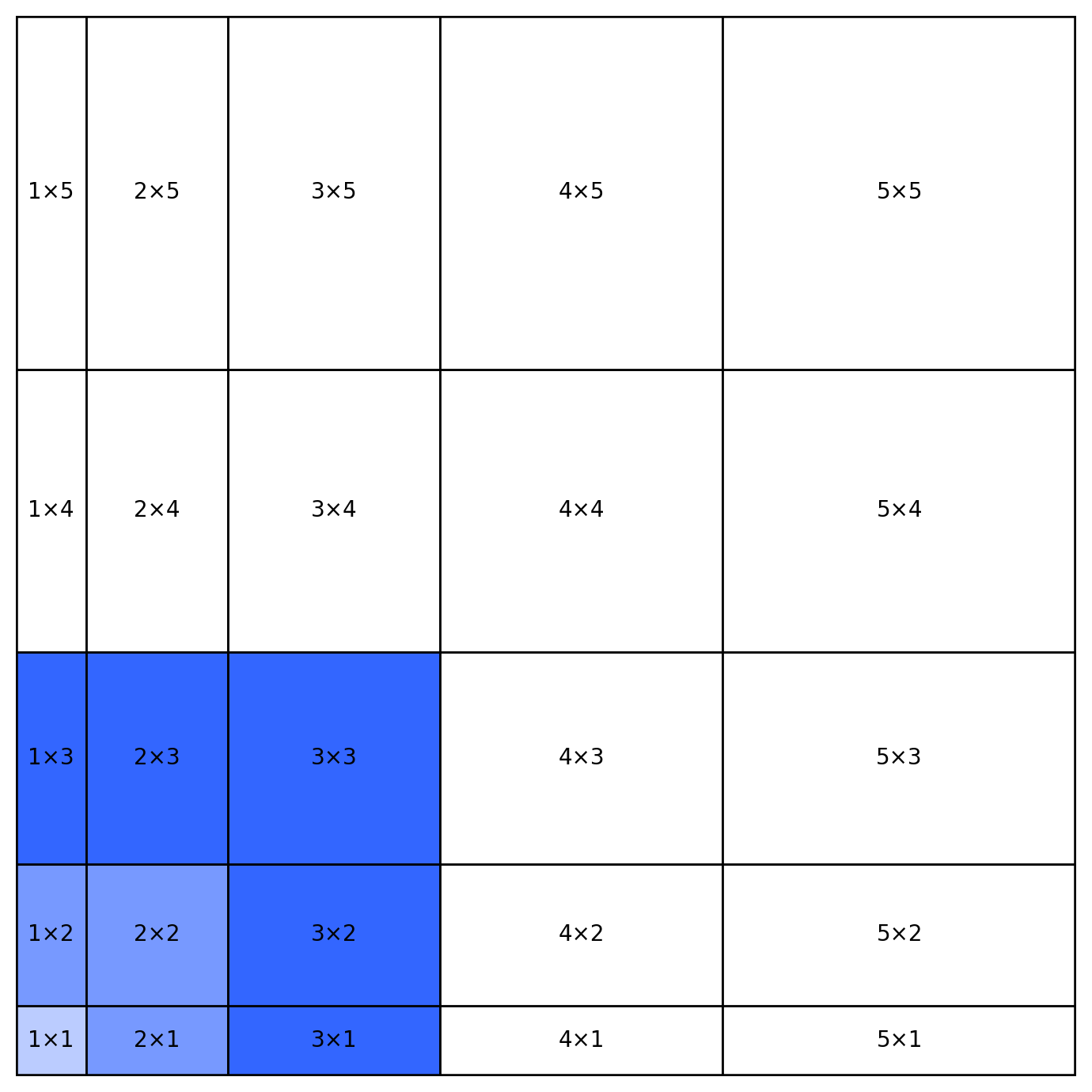
مساحت این لایه چقدر است؟

به همان لایه‌ی L-شکل نگاه کنیم.

برای رفتن از مرحله‌ی $k-1$ به مرحله‌ی $k$ چه چیزی اضافه کردیم؟

• یک نوار عمودی با عرض $k$ و طول $1+2+\cdots+k$،
• یک نوار افقی با همان ابعاد.

اگر این دو نوار را جداگانه حساب کنیم، مجموع مساحتشان می‌شود:

$$2 \times k(1+2+\cdots+k).$$

اما یک نکته هست: گوشه‌ی مشترک — یعنی مربعِ $k\times k$ — در این جمع دوبار شمرده شده است.

پس باید یک‌بار آن را کم کنیم.

در نتیجه، مساحت کل لایه برابر است با:

$$2k(1+2+\cdots+k) - k^2.$$

حالا فقط همین را ساده می‌کنیم.

می‌دانیم:

$$1+2+\cdots+k = \frac{k(k+1)}{2}.$$

پس داریم:

$$2k \cdot \frac{k(k+1)}{2} - k^2 = k^2(k+1) - k^2 = k^3.$$

و این دقیقاً همان چیزی است که می‌خواستیم.

---

کنار هم گذاشتنِ همه‌ی لایه‌ها

حالا از $k=1$ تا $k=n$، همه‌ی این لایه‌ها را روی هم بگذارید.

کل مربعِ بزرگ با ضلع

$$1+2+\cdots+n$$

از همین لایه‌ها ساخته شده است.

پس مساحت کل مربع برابر است با:

$$1^3 + 2^3 + 3^3 + \cdots + n^3.$$

اما این همان مساحت

$$(1+2+\cdots+n)^2$$

است.

---

نتیجه

در نتیجه، نه از راهِ یک محاسبه‌ی تصادفی، بلکه از راهِ یک ساختارِ هندسیِ لایه‌به‌لایه داریم:

$$1^3 + 2^3 + \cdots + n^3 = \left(1+2+\cdots+n\right)^2.$$

این تساوی صرفاً یک اتحاد جبری نیست؛
بیانِ این حقیقت است که یک مربعِ بزرگ، از پوسته‌هایی با حجم‌های مکعبی ساخته شده است.