مسئلهٔ برچسبگذاری یالهای گراف کامل
روی یالهای یک گراف کامل ، اعداد را نوشتهایم،
بهطوریکه در هر مثلثِ گراف:
- عددِ روی دو یال با هم برابر است،
- و عددِ روی یالِ سوم از آن دو عدد بزرگتر است.
گراف دستِ بالا چند راس میتواند داشته باشد؟
اولین برخورد با مسئله: از حالتهای ساده شروع کنیم
وقتی برای اولین بار با یک مسئلهٔ جدید روبهرو میشویم، معمولاً ساختار آن هنوز برایمان شفاف نیست.
در چنین موقعیتی، یکی از بهترین استراتژیها این است که مسئله را در سادهترین حالتهای ممکن امتحان کنیم؛
یعنی بهجای حملهٔ مستقیم به حالت کلی، ابتدا سراغ مقادیر کوچک برویم.
این کار دو فایدهٔ مهم دارد:
- ابهام مسئله کمتر میشود و میفهمیم دقیقاً با چه نوع محدودیتی طرف هستیم؛
- الگوها و رفتارهایی ظاهر میشوند که بعداً در حل کلی راهگشا هستند.
به این رویکرد معمولاً میگویند:
دستبهکار شدن و آلودن دستها (get your hands dirty)
یعنی بهجای فکر کردن انتزاعی و دور از مثال،
واقعاً با مسئله کار کنیم، مثال بسازیم، و ببینیم چه چیزهایی ممکن است و چه چیزهایی نه.
بررسی مسئله برای های کوچک
گام اول: بررسی حالت
در حالت ، فقط اجازه داریم عدد را روی یالها بنویسیم.
از طرفی، شرط مسئله میگوید که در هر مثلث:
- عدد دو یال برابر است،
- و عدد یال سوم از آن دو بزرگتر است.
اما وقتی تنها عدد مجاز باشد، هیچ عددی بزرگتر از وجود ندارد. پس نتیجهٔ مهمی میگیریم:
در گراف نمیتواند حتی یک مثلث وجود داشته باشد.
چون اگر مثلثی وجود داشته باشد، شرط «بزرگتر بودن یال سوم» بلافاصله نقض میشود. بنابراین در حالت :
- گراف میتواند حداکثر رأس داشته باشد.
این اولین دادهٔ عددی ماست.
فعلاً شاید ساده بهنظر برسد، اما همین بررسیهای کوچک هستند که مسیر حل کلی را روشن میکنند.
گام دوم: بررسی حالت
اولین نشانههای ساختار
حالا اجازه داریم روی یالها فقط دو عدد بنویسیم و . شرط مثلث را دوباره، اما دقیقتر، در این حالت بخوانیم:
- در هر مثلث، دو یال عدد برابر دارند،
- و یال سوم عددی بزرگتر از آن دو دارد.
از آنجا که فقط دو عدد داریم، نتیجهٔ مهم و فوری این است:
در هر مثلث، دقیقاً دو یال با عدد 1
و یک یال با عدد 2 وجود دارد.
گراف با 3 رأس
گراف کامل روی 3 رأس فقط یک مثلث دارد.
میتوانیم بهراحتی یکی از یالها را 2 بگذاریم و دو تای دیگر را 1.
پس گراف با رأس ممکن است.
گراف با 4 رأس
گراف کامل روی 4 رأس، چهار مثلث دارد.
سؤال طبیعی این است:
آیا میتوان یالهای 2 را طوری انتخاب کرد
که هر مثلث دقیقاً یکی از آنها را در خود داشته باشد؟
یک انتخاب جالب این است:
- رأسها را به دو جفت تقسیم کنیم،
- یال بین هر جفت را با عدد 2 برچسب بزنیم،
- بقیهٔ یالها را 1 بگذاریم.
در این حالت:
- هر مثلث دقیقاً شامل یکی از این یالهای 2 است،
- و شرط مسئله در همهٔ مثلثها برقرار میماند.
پس گراف با 4 رأس هم امکانپذیر است.
آیا 5 رأس هم ممکن است؟
اینجا جایی است که ساختار شروع به مقاومت میکند.
اگر بخواهیم شرط «هر مثلث دقیقاً یک یال 2 دارد» را نگه داریم، باید یالهای 2 را آنقدر منظم پخش کنیم که:
- هیچ مثلثی بدون یال 2 نماند،
- و هیچ مثلثی بیش از یکی نگیرد.
اما در گراف کامل روی 5 رأس:
- تعداد مثلثها بهشدت زیاد میشود،
- و هر یال در مثلثهای متعددی شرکت میکند.
با کمی امتحان کردن (یا کمی جلوتر با استدلال دقیقتر)، میبینیم که:
هر چیدمانی از یالهای 2 در نهایت
یا یک مثلث بدون یال 2 میسازد،
یا مثلثی با دو یال 2.
و هر دو حالت، شرط مسئله را نقض میکنند.
آنچه تا اینجا بهدست آوردیم:
- برای :
- با رأس هم ممکن است،
- اما با رأس دیگر نمیشود شرط مثلث را حفظ کرد.
آیا ایدهٔ استقرا جواب میدهد؟
ساختن گراف بزرگتر از روی گراف کوچکتر
بعد از بررسی حالتهای و ، یک الگو کمکم خودش را نشان میدهد: هر بار که تعداد اعداد مجاز روی یالها (مقدار ) یک واحد بیشتر میشود، بهنظر میرسد بتوان اندازهٔ گراف را دو برابر کرد.
این مشاهده ما را به یک سؤال طبیعی میرساند:
آیا میتوان از یک گراف کامل با برچسبهای تا ،
یک گراف کامل بزرگتر با برچسبهای تا ساخت
که شرط مثلث همچنان برقرار بماند؟
اگر پاسخ مثبت باشد، ایدهٔ استقرا بهطور جدی وارد بازی میشود.
فرض استقرا
فرض کنید برای عدد ، یک گراف کامل وجود دارد که:
- یالهای آن با اعداد برچسبگذاری شدهاند،
- شرط مسئله در تمام مثلثها برقرار است،
- و این گراف رأس دارد.
میخواهیم با استفاده از همین گراف، یک گراف کامل جدید با برچسبهای بسازیم که تعداد رأسهایش بیشتر باشد.
یک تغییر ساده اما کلیدی
اولین حرکت ما بسیار ساده است، اما مهم:
- تمام برچسبهای یالهای گراف اولیه را یک واحد افزایش میدهیم.
یعنی:
- یالهایی که عدد داشتند، حالا میگیرند،
- یالهای تبدیل به میشوند،
- و بهطور کلی، هر عدد به تبدیل میشود.
بعد از این تغییر:
- همهٔ برچسبها در بازهٔ تا قرار دارند،
- و شرط مثلث همچنان برقرار است
(چون فقط یک انتقال یکنواخت روی اعداد انجام دادهایم).
دو نسخه کنار هم
حالا از این گرافِ جدید، دو نسخهٔ کاملاً یکسان میسازیم:
- هر دو نسخه گراف کاملاند،
- هر دو دقیقاً همان برچسبگذاری را دارند،
- و هیچ رأسی میان دو نسخه مشترک نیست.
تا اینجا، هر نسخه بهتنهایی تمام شرایط مسئله را ارضا میکند.
اتصال دو بخش با یالهای 1
اکنون مرحلهٔ تعیینکننده میرسد.
- هر رأس از نسخهٔ اول را به هر رأس از نسخهٔ دوم وصل میکنیم،
- و تمام یالهای بین این دو بخش را با عدد برچسب میزنیم.
در نتیجه:
- گراف نهایی هنوز یک گراف کامل است،
- و برچسبهای یالها دقیقاً اعداد تا را تشکیل میدهند.
بررسی شرط مثلث
حالا باید مطمئن شویم که در تمام مثلثهای گراف جدید،
شرط مسئله برقرار است.
سه حالت ممکن داریم:
۱. مثلثهایی که کاملاً در یکی از دو نسخهاند
در این حالت:
- هر سه رأس مثلث در یک نسخه قرار دارند،
- و یالهای آن فقط برچسبهای تا دارند.
چون این گراف از فرض استقرا آمده، شرط مسئله در این مثلثها برقرار است.
۲. مثلثهایی که دو رأس در یک نسخه و یک رأس در نسخهٔ دیگر دارند
در چنین مثلثی:
- دو یال، یالهای بین دو نسخهاند و برچسب دارند،
- یال سوم داخل یکی از نسخههاست و عددی بزرگتر از دارد.
پس در این مثلث:
- دو یال عدد برابر () دارند،
- و یال سوم عددی بزرگتر از آنها دارد.
دقیقاً همان چیزی که شرط مسئله میخواهد.
نتیجهٔ استقرایی
به این ترتیب، از یک گراف کامل با رأس و برچسبهای تا ، یک گراف کامل جدید با:
- برچسبهای تا ،
- و تعداد رأسهای
ساختهایم که شرط مسئله را ارضا میکند.
این یعنی:
هر بار که یک واحد افزایش پیدا میکند،
میتوان حداکثر تعداد رأسها را دو برابر کرد.
این ساخت استقرایی نهتنها امکانپذیر است، بلکه کاملاً با مثالهای کوچک و هم سازگار است.
یعنی میتوان گرافی با راسی ساخت که برچسبهای تا داشته باشد و شرط مثلث گفته شده برقرار باشد. (چرا که برای میتوان گراف راسی ساخت و هر بار که زیاد میشود اندازهی گراف دوبرابر میشود).
در گام بعدی، میتوانیم ببینیم:
- آیا این حدِ دو برابر شدن بهینه است؟
- و آیا واقعاً بیش از این نمیتوان گراف را بزرگتر کرد؟
گام بعد: کران بالا
چرا گراف کامل با رأس دیگر شدنی نیست؟
تا اینجا یک ساخت استقرایی دیدیم که نشان میداد با افزایش میتوان گراف را بزرگتر کرد (حتی بهصورت تقریباً دو برابر).
اما اگر هدف ما «حداکثر» باشد، فقط ساختن مثال کافی نیست؛ باید نشان دهیم بزرگتر از یک حد مشخص دیگر امکانپذیر نیست.
اینجاست که یک نکتهٔ آموزشی مهم رخ میدهد:
استقرا فقط ابزار اثبات «وجود» نیست؛
برای اثبات «عدم وجود» هم میتواند بسیار قدرتمند باشد.
یعنی میتوانیم با استقرا ثابت کنیم که: «هیچ آرایشی با این اندازه وجود ندارد.»
هدف
میخواهیم ثابت کنیم:
برای گراف کامل با رأس،
هیچ برچسبگذاری با اعداد وجود ندارد
که شرط مثلث مسئله را ارضا کند.
چرا از استقرای قوی استفاده میکنیم؟
وقتی میخواهیم «عدم امکان» را ثابت کنیم، معمولاً نیاز داریم از این واقعیت استفاده کنیم که:
اگر یک ساختار خیلی بزرگ وجود داشته باشد،
داخلش یک زیرساختار کوچکتر هم پیدا میشود که همان خاصیت را به ارث میبرد.
پس اگر بدانیم در اندازهٔ کوچکتر چنین چیزی ناممکن است، میتوانیم تناقض بسازیم.
این دقیقاً جایی است که استقرای قوی طبیعی بهنظر میرسد.
فرض استقرا
فرض میکنیم گزارهٔ زیر برای عدد درست است:
هیچ برچسبگذاری با اعداد
برای گراف کامل با رأس وجود ندارد
که شرط مثلث مسئله را ارضا کند.
گام استقرا: تلاش برای رسیدن به تناقض
حالا باید نشان دهیم که نتیجهٔ متناظر برای هم درست است؛ یعنی نمیتوان یالهای را با برچسبهای تا برچسبگذاری کرد بهطوری که شرط مثلث گفته شده برقرار باشد.
برای این کار از یک تکنیک کلاسیک استفاده میکنیم: برهان خلف.
فرض کنید بر خلاف ادعای ما، چنین برچسبگذاریای وجود داشته باشد.
یعنی فرض میکنیم:
- یک گراف کامل با رأس داریم،
- یالهای آن با اعداد برچسبگذاری شدهاند،
- و در هر مثلث، دقیقاً دو یال همبرچسباند و یال سوم برچسبی بزرگتر دارد.
از اینجا به بعد هدف ما این است که از دل همین فرض، بهنوعی یک زیرگراف «بهاندازهی کافی بزرگ ()» استخراج کنیم که فقط از برچسبهای تا استفاده کند، و آنگاه با فرض استقرا به تناقض برسیم.
بیرون کشیدن زیرگرافهای ممنوعه از اطراف یک رأس
ایدهٔ کلیدی: به «طبقهبندی همسایهها بر حسب برچسب» نگاه کنیم
طبق برهان خلف، فرض میکنیم یک برچسبگذاری معتبر روی گراف کامل با برچسبهای تا وجود دارد.
حالا یک رأس دلخواه را انتخاب میکنیم و آن را مینامیم.
تمام رأسهای دیگر به وصلاند، و هر یال یکی از برچسبهای تا را دارد.
پس میتوانیم همسایههای را بر اساس برچسب یالِ وصلکننده دستهبندی کنیم.
برای هر تعریف میکنیم:
- = تعداد رأسهایی که با یالی با برچسب به وصل شدهاند.
پس داریم: چون در دقیقاً رأسِ دیگر غیر از وجود دارد.
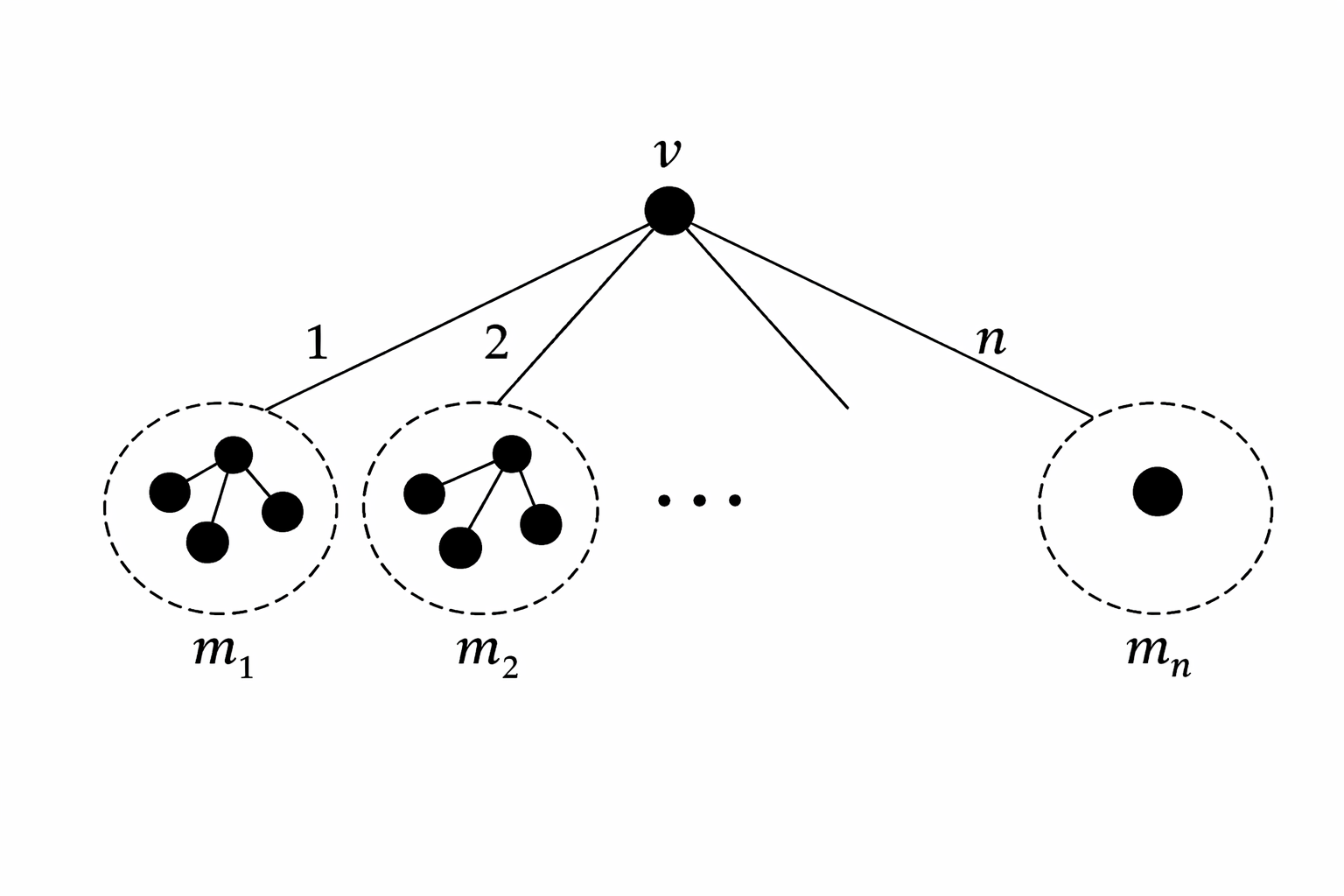
مشاهدهٔ اول: زیرگرافِ همسایههای برچسب
به مجموعهٔ رأسهایی نگاه کنید که با یالِ برچسب به وصل شدهاند.
این مجموعه را مینامیم، بنابراین .
حالا دو رأس دلخواه را بردارید.
در مثلث داریم:
- یال برچسب دارد،
- یال هم برچسب دارد.
پس در این مثلث، «دو یال برابر» همین دو یال هستند،
و بنابراین یال سوم یعنی باید برچسبی بزرگتر از داشته باشد.
یعنی:
هیچ یالی بین دو رأسِ نمیتواند برچسب داشته باشد.
پس در زیرگراف کاملِ القاشده روی ، برچسبها فقط از مجموعهٔ میآیند.
ترفند مهم: کم کردن یک واحد از همهٔ برچسبها
حالا یک حرکت فکری انجام میدهیم که در این نوع مسائل خیلی کلیدی است:
- روی همهٔ یالهای داخل ، از برچسبها یک واحد کم میکنیم.
آنگاه برچسبهای تبدیل میشوند به .
و نکتهٔ حیاتی این است که:
شرط مثلث با این «جابجایی یکنواخت» خراب نمیشود.
چون در هر مثلث، فقط مقایسهٔ «برابر بودن دو یال» و «بزرگتر بودن سومی» مهم است؛
و کم کردن یک عدد ثابت از همهٔ یالهای یک زیرگراف، این روابط را حفظ میکند.
پس نتیجه میگیریم:
- زیرگراف کامل روی رأس را میتوان با برچسبهای تا طوری برچسبگذاری کرد که شرط مثلث برقرار باشد.
اما این دقیقاً همان چیزی است که فرض استقرا آن را برای اندازهٔ غیرممکن میداند.
پس اگر باشد، به تناقض میرسیم. بنابراین:
همین ایده برای و بقیهٔ دستهها
حالا به دستهٔ دوم نگاه میکنیم:
- مجموعه برابر مجموعهٔ رأسهایی که با یالِ برچسب به وصلاند،
- بنابراین
اگر باشند، در مثلث داریم:
- , ، پس یال سوم یعنی باید بزرگتر از باشد.
پس در زیرگراف کامل روی ، برچسبها فقط از میآیند.
حالا از همهٔ این برچسبها دو واحد کم میکنیم و به برچسبهای میرسیم، و باز هم شرط مثلث حفظ میشود.
بنابراین اگر خیلی بزرگ باشد، یک نمونهٔ ممنوعه برای تولید میشود؛ پس:
الگوی کلی
بهطور کلی برای هر :
- = همسایههایی که با برچسب به وصلاند،
- در هر مثلث با ، دو یال برابر هستند،
- پس یال سوم باید برچسبی بزرگتر از داشته باشد.
پس در زیرگراف کامل روی ، برچسبها از مجموعهٔ هستند.
حالا اگر از همهٔ این برچسبها واحد کم کنیم، به برچسبهای میرسیم، و شرط مثلث همچنان برقرار میماند.
پس اگر از حدی بزرگتر شود، به یک نمونهٔ ممنوعه برای میرسیم. بنابراین:
جمعبندی: شمارش همسایهها
اکنون تعداد کل همسایههای برابر است با:
ولی طبق نامساویهای بالا داریم:
و میدانیم:
پس:
اما از طرف دیگر، در گراف تعداد همسایههای دقیقاً است.
یعنی باید داشته باشیم:
که با نامساوی بالا تناقض دارد.
پس فرض خلف ما نادرست بوده است.
نتیجهٔ نهایی کران بالا
بنابراین:
گراف کامل با رأس نمیتواند چنین برچسبگذاریای داشته باشد.
و در نتیجه، حداکثر تعداد رأسهای گرافی که میتواند شرط مسئله را ارضا کند برابر است با: