اعداد مختلط
گسترش طبیعی مفهوم عدد از محور حقیقی به سراسر صفحه
معرفی دستگاه اعداد مختلط گسترش طبیعی اعداد حقیقی از یک محور یکبعدی به صفحهای دوبعدی است — صفحهای که در آن، جمع و ضرب معناهایی هندسی و روشن پیدا میکنند.
از محور حقیقی تا صفحهٔ دوبعدی
یک عدد مختلط را میتوانیم یک نقطه در صفحه در نظر بگیریم؛ و یا با تعبیری دیگر برداری که از مبدأ به آن نقطه کشیده شدهاست.
اگر مختصات این نقطه را $ (x_0, y_0) $ بنامیم، میگوییم عدد مختلطی که این نقطه را نشان میدهد، دارای:
- قسمت حقیقی (طول) $x_0$
- قسمت موهومی (عرض) $y_0$
است. پس میتوانیم یک عدد مختلط را بهصورت یک زوجِ مرتب بنویسیم:
\[z = (x_0, y_0)\]
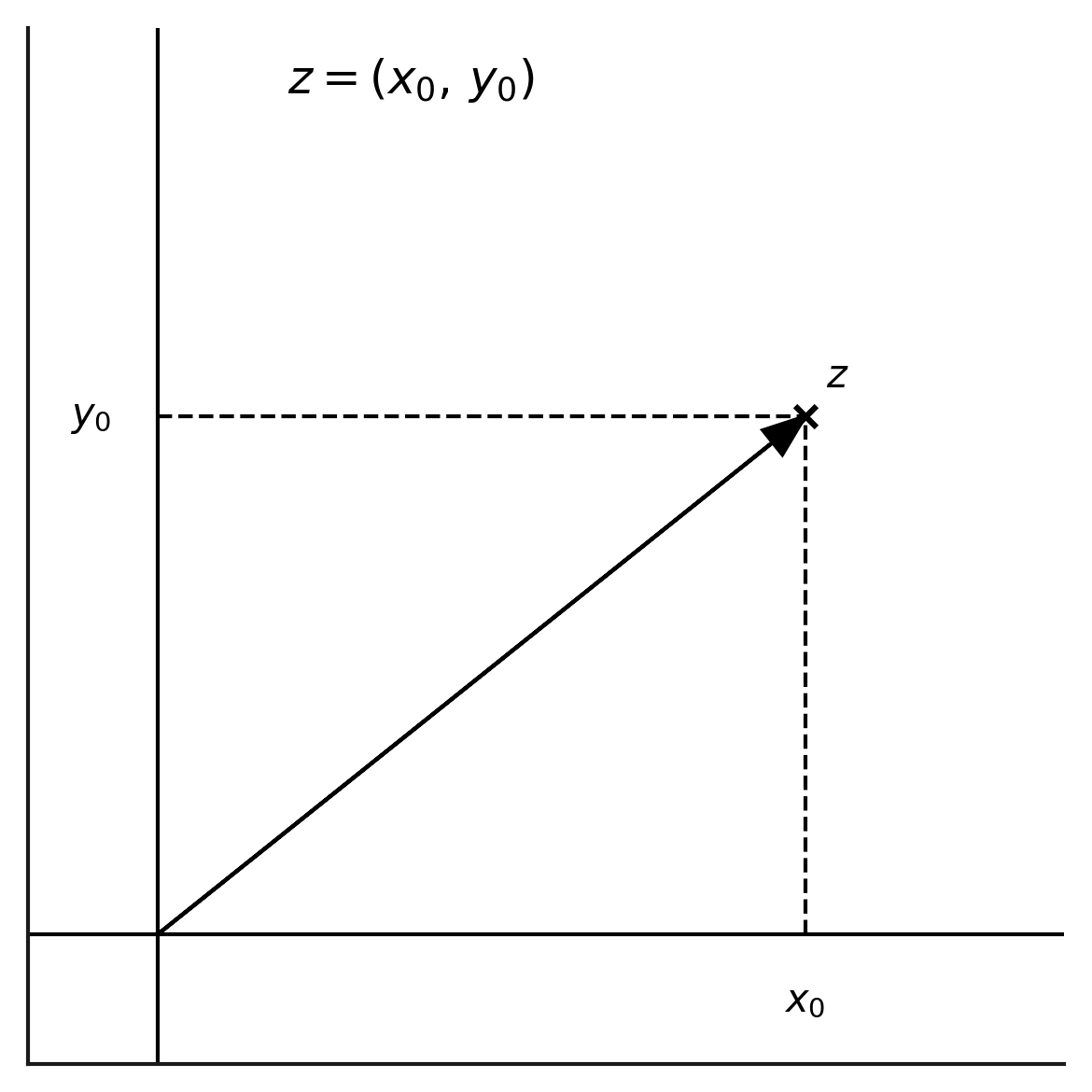
در این برداشت، اعداد حقیقی نیز بهطور طبیعی در میان اعداد مختلط جای میگیرند؛
زیرا هر عدد حقیقی $a$ همان نقطهٔ $(a, 0)$ در صفحه است — یعنی همان برداری که روی محور افقی قرار دارد.
تعریف طبیعی جمع
حال اگر بخواهیم جمع را در این صفحه تعریف کنیم، سرراستترین راه آن است که جمع را همانند جمع دو بردار در نظر بگیریم.
این تعریف، همان رفتار شناختهشدهٔ جمع روی محور حقیقی را به شکلی طبیعی به کل صفحه گسترش میدهد.
اگر
\[z_1 = (x_1, y_1), \qquad z_2 = (x_2, y_2)\]دو عدد مختلط باشند، جمع آنها چنین تعریف میشود:
\[z_1 + z_2 = (x_1 + x_2,\; y_1 + y_2)\]این همان قاعدهٔ آشنای جمع بردارهاست:
بردار دوم را از سرِ بردارِ اول آغاز میکنیم و نقطهٔ پایان، حاصل جمع است.
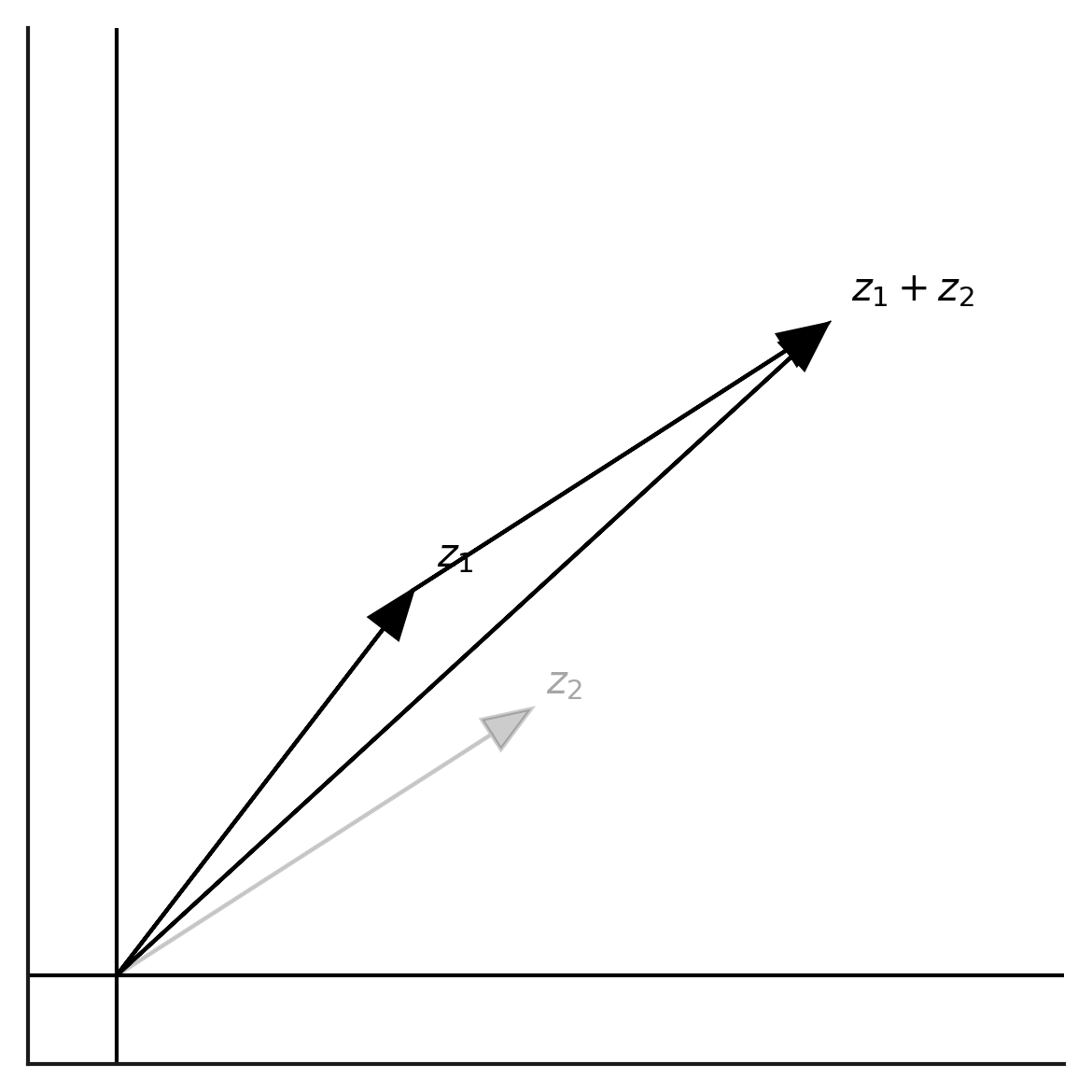
تعریف ضرب: دوران بردارها
پس از آنکه جمع را بهصورت جمع بردارها تعریف کردیم، اکنون نوبت به ضرب میرسد. تعریف ضرب در صفحه مانند جمع سرراست نیست؛ اما یک برداشت هندسی روشن دارد که آن را کاملاً طبیعی میکند.
هر عدد مختلط — یعنی هر نقطه یا بردار در صفحه — با دو ویژگی توصیف میشود:
- طولِ بردار: $\lvert z\rvert$
- زاویهای که با جهت مثبت محور حقیقی میسازد: $\theta$
ایدهٔ اصلی برای تعریف ضرب این است که:
- طولِ حاصلضرب برابر باشد با حاصلضرب طولهای دو عدد،
- زاویهٔ حاصلضرب برابر باشد با مجموع زاویههای دو عدد.
به بیان هندسی:
وقتی دو عدد مختلط $z_1$ و $z_2$ را در هم ضرب میکنیم، بردار حاصلضرب، برداری است که
- ابتدا به اندازهٔ $\lvert z_1\rvert \lvert z_2\rvert$ کشش پیدا کرده،
- و سپس به اندازهٔ $\theta_1 + \theta_2$ چرخیده است.
این تعریف، هرچند در نگاه اول ساده نیست، اما با ضرب اعداد حقیقی کاملاً سازگار است و آن مفهوم را بهطبیعتیترین شکل به سراسر صفحه گسترش میدهد.
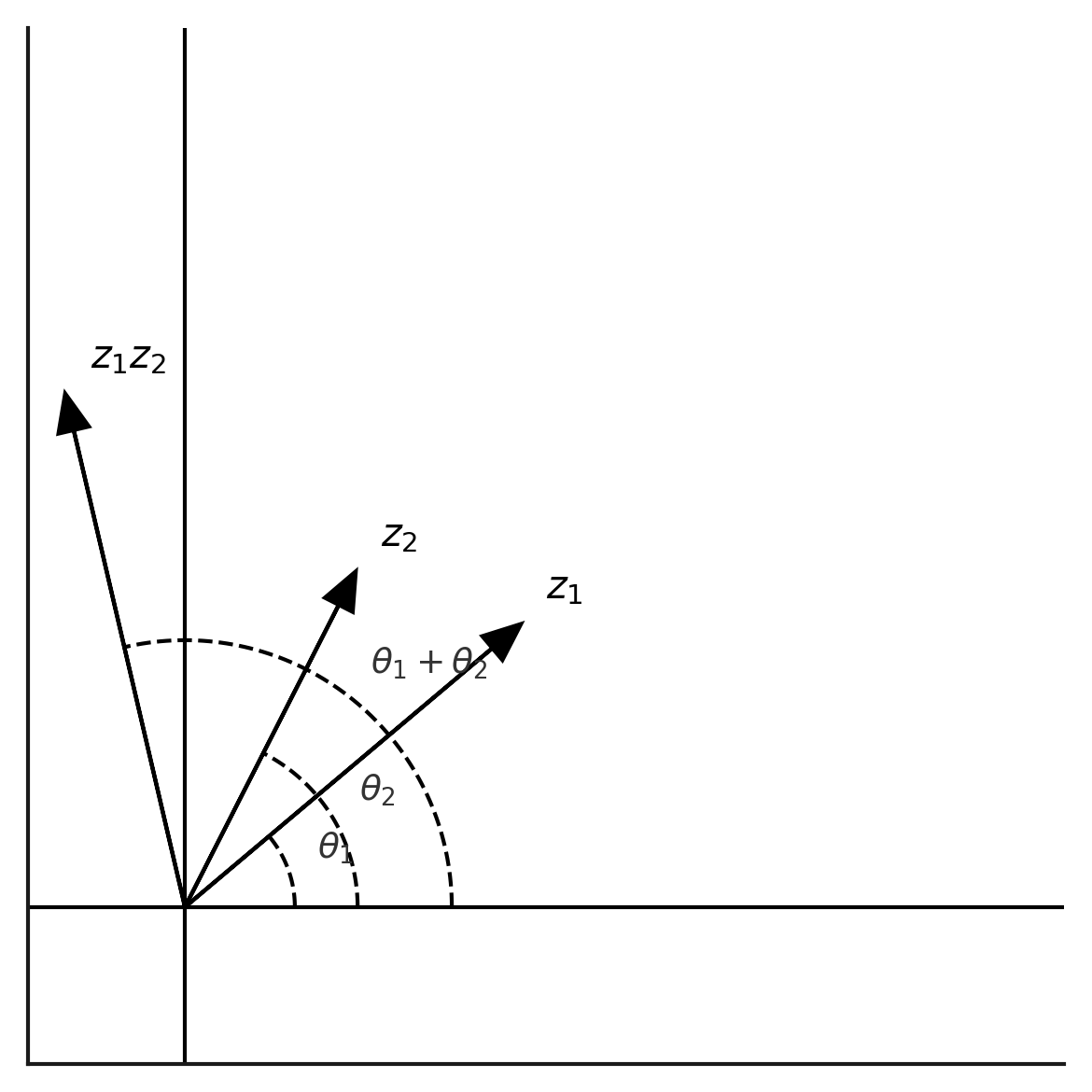
برای اطمینان از اینکه تعریف هندسیِ ضرب با ضربِ معمولی اعداد حقیقی سازگار است، دو عدد حقیقی $a$ و $b$ را در نظر میگیریم. در صفحهٔ مختلط این دو عدد همان بردارهای
\[(a,0), \qquad (b,0)\]هستند. زاویهٔ هر دو بردار نسبت به محور حقیقی یا $0$ است (اگر مثبت باشند) یا $\pi$ (اگر منفی باشند). بنابراین زاویهٔ حاصلضرب برابر است با جمع این زاویهها:
-
اگر $a$ و $b$ هر دو مثبت باشند: \(0 + 0 = 0\)
-
اگر یکی منفی و دیگری مثبت باشد: \(\pi + 0 = \pi\)
که یعنی حاصلضرب روی محور حقیقی و در جهت منفی قرار میگیرد. -
اگر هر دو منفی باشند:
\(\pi + \pi = 2\pi = 0\)
(چرخش یک دور کامل) و نتیجه دوباره در جهت مثبت محور خواهد بود.
از طرف دیگر، طول بردار حاصلضرب برابر است با
\[\lvert a\rvert\,\lvert b\rvert = \lvert ab\rvert.\]پس بردار حاصلضرب دقیقاً همان نقطهٔ
\[(ab, 0)\]را نشان میدهد — درست همان نتیجهای که از ضربِ اعداد حقیقی انتظار داریم.
عدد یکهی موهومی ($i$) و معنای هندسی آن
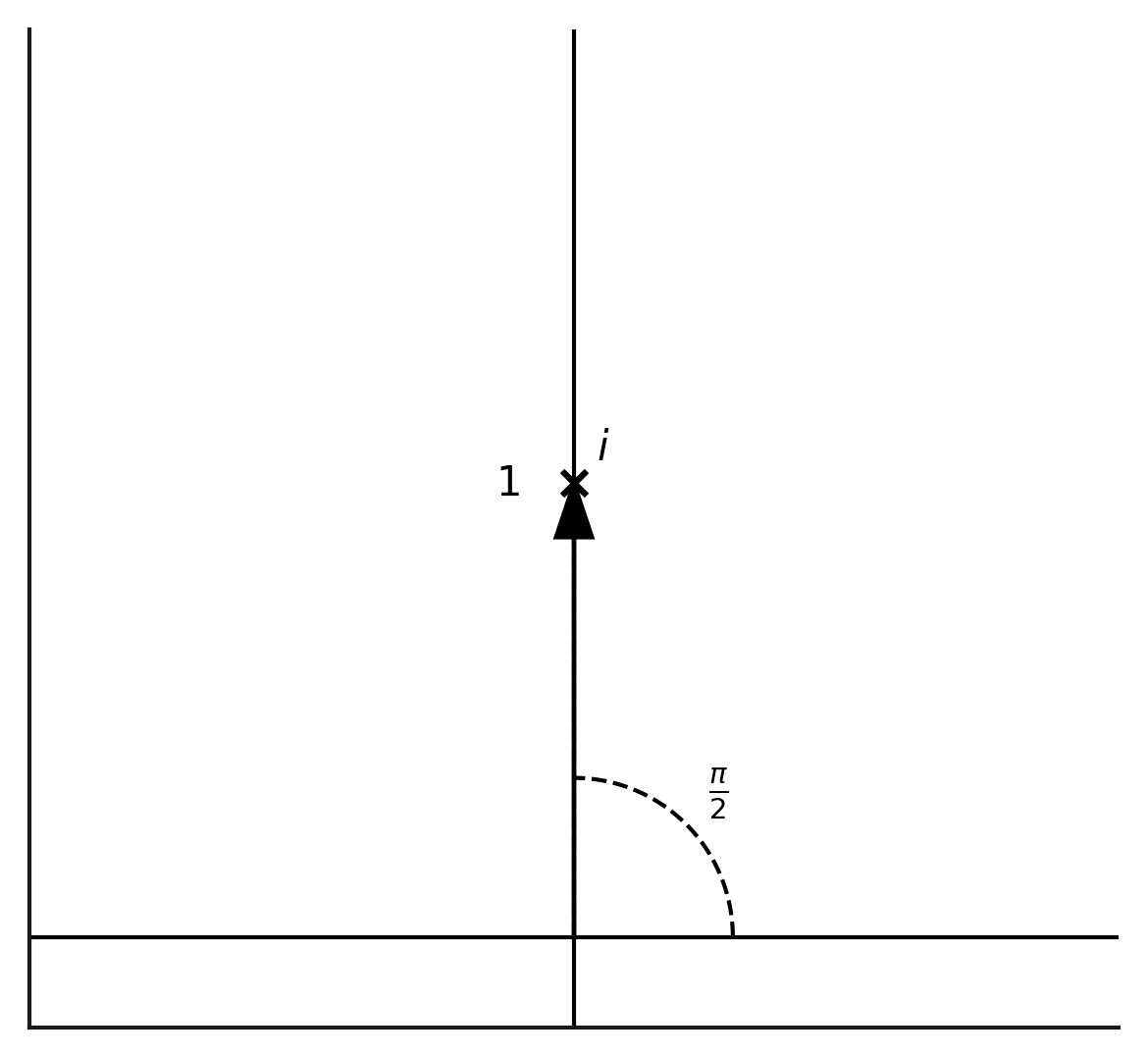
تا اینجا اعداد مختلط را بهصورت نقطه یا بردار در صفحه دیدیم. در این دستگاه، یکی از بنیادیترین بردارها، بردار
\[i = (0, 1)\]است؛ یعنی برداری که دقیقاً بر محور عمودی و با طول ۱ از مبدأ بالا میرود. این بردار زاویهای برابر با $\frac{\pi}{2}$ با محور حقیقی میسازد. بر اساس تعریف هندسیِ ضرب، ضرب یک عدد مختلط در $i$ یعنی:
- کشش طول به اندازهٔ $\lvert i\rvert = 1$ (پس طول تغییر نمیکند)،
- چرخش به اندازهٔ $\frac{\pi}{2}$.
به بیان دیگر: ضرب در $i$ یعنی چرخش پادساعتگردِ ۹۰ درجه.
بررسی $i \times i$
بردار $i$ طول یک و زاویهٔ $\frac{\pi}{2}$ دارد. بنابراین در ضرب آن با خودش:
- طول جدید برابر است با
\(\lvert i\rvert\,\lvert i\rvert = 1\) - زاویهٔ جدید برابر است با
\(\frac{\pi}{2} + \frac{\pi}{2} = \pi\)
و برداری با طول یک و زاویهٔ $\pi$ همان نقطهٔ $(-1, 0)$ در صفحه است. پس به نتیجهٔ مشهور میرسیم:
\[i^2 = -1.\]این نتیجه فقط یک قانون جبری نیست؛ بلکه پیامد مستقیم تعریف هندسیِ ضرب است: چرخش ۹۰ درجه + دوباره چرخش ۹۰ درجه -> چرخش ۱۸۰ درجه -> رسیدن به $-1$.